Тёмный треугольник со сторонами

— нижнее основание призмы,

— ортогональная проекция верхнего основания на плоскость нижнего.
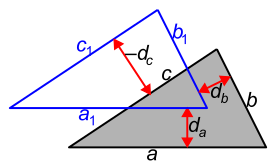
Пусть

— расстояние между прямыми

и

со знаком: если

лежит по ту же сторону от

, что и тёмный треугольник, припишем

знак плюс, если по другую — минус. Аналогично введём

. На картинке показана ситуация, когда

.
Тогда

равны соответственно

, делённым на высоту призмы. Задача превращается в планиметрическую и сводится к доказательству

а с учётом теоремы синусов —

Но это — утверждение о том, что сумма площадей вот этих трёх параллелограммов (со знаками, по тому же принципу) равна нулю:




