(Решение)
Возьмём квадрат

. Его можно разбить на

квадрата
, значит, в нём

закрашенных клеток. Его также можно разбить на

прямоугольника

(в совокупности имеют

закрашенных клеток) и центральный «глазок»

, как на картинке. Значит, все клетки «глазка» закрашены.
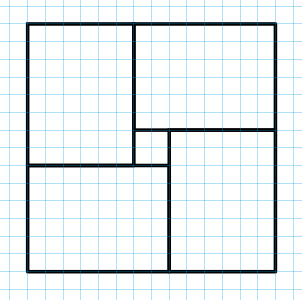
Двигая эту конструкцию и всё время закрашивая глазок, легко получим полностью закрашенный квадрат
, противоречащий условию.
Должен признать, задача вышла так себе, а у вас очень хорошее решение. У меня хуже и вообще на строгое не тянет:
Предположим, закраска существует. Рассмотрим квадрат

и в нем подквадрат

. В большем должно быть ровно

заражённых клеток, в меньшем -

. Значит, в уголке 73 закрашенные клетки. Поскольку это верно для любого квадрата

, то в любой полоске

должно быть не менее 36 закрашенных клеток. Но тогда квадрат

с одной стороны, имеет

клеток, а с другой - не менее

клеток, откуда противоречие.



