Да, система совместная.
Правая часть нулевая!
Не, это совсем не задача с линейной системой, а задача на поиск нулевых сингулярных чисел и соответсвующих им сингулярных векторов.
Как решать - зависит от того, какая точность Вас интересует и какова размерность задачи.
Например, если Вас

вычислительной сложности не напрягает и

памяти у Вас имеется, то надо просто посчитать нулевые сингулярные вектора. Тогда решением будет любая линейная комбинация всех правых сингулярных векторов, которые соответсвуют нулевым сингулярным значениям.
Если столько ресурсов нет, то надо смотреть в сторону итерационных алгоритмов Ланцоша и Арнольди, возможно с рестартом. При больших размерностях матриц не забывать, что численно вычисленное скалярное произведение двух очень больших по размерности векторов имеет большую численную ошибку, которая накапливается в таких итерационных методах, если на это не обращать внимание.
Если задача не рыба, не мясо, или матрица не большая, но хочется решать быстро, то надо делать
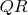
c rank-revealing, и использовать верхний недотреугольник для получения решения.