разбиваем на 7 подгрупп по 6 человек
То есть, взяв наугад по человеку из каждой подгруппы, обязательно получим нужную семерку? Но кто-нибудь из 42 может не знать шестерых, и тогда один человек в семерке может не вписаться.
-- 20.12.2023, 01:45 --Такой вариант. Возьмем одного человека. Допустим, он не знает шесть человек. Из

оставшихся ему знакомых выберем второго. Допустим, второй тоже не знает шесть человек, и пусть пересечение множеств незнакомцев первого и второго пусто. Из

оставшихся выбираем третьего общего знакомого. Пусть и у него шесть незнакомых, и пересечение множеств незнакомцев всех трёх пусто. Из

оставшихся выбираем четвертого. Рассуждаем также и выбираем из

оставшихся пятого, а из

- шестого. Седьмого выбрать не получится, потому что

. Но такого не может быть, т.к. у каждого из выбранных таким образом шестерых оказалось бы по
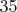
знакомых. Поэтому пересечение множеств незнакомцев не пусто, и седьмой обязательно найдется.



