I want to prove that if
![$f:[a,b] \to \mathbf{R}$ $f:[a,b] \to \mathbf{R}$](https://dxdy-02.korotkov.co.uk/f/d/4/1/d41264ab53d000b8e9f36d70ee630eb082.png)
is a bounded continuous function then the sequence of Riemann sum (as the partition is getting finer and finer) converges.
My attempt:
If we can prove that Riemann sum is a Cauchy sequence (sequence as the partition is getting finer and finer), then uniqueness of limit ensures that it converges.
Let
![$P^{(n)} = \left( \{[x_i^{(n)}, x_{i+1}^{(n)}]\}, t_i^{(n)} \in [x_i^{(n)}, x_{i+1}^{(n)}]\right)$ $P^{(n)} = \left( \{[x_i^{(n)}, x_{i+1}^{(n)}]\}, t_i^{(n)} \in [x_i^{(n)}, x_{i+1}^{(n)}]\right)$](https://dxdy-04.korotkov.co.uk/f/b/9/1/b910bef1b33bdb1545cfc0e1b948183882.png)
be a sequence of partitons. Such that:
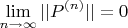
Consider a partition
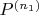
and its refinement
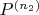
, that is the latter is obtained by inserting more points in between the points of the former.
Let us try to obtain Cauchy criterion:
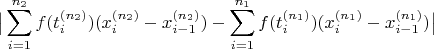
As
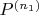
is coarser, we can take its norm and get an inequality:
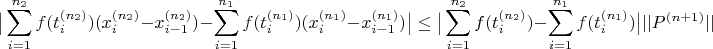
I’m having issues in getting an upper bound for

because one of the sum goes upto

while the other upto

.
Can you please give me a hint and carry me on over this?