Я пытаюсь показать (не доказать, потому что я хочу сначала хотя бы эвристически получить нужный результат) ЦПТ как предел бесконечных сверток, и вроде такой способ дает нужный результат. Но когда я пытаюсь его обобщить на то, чтобы получить еще и скорость сходимости к гауссиане (теорему Берри-Эссеена), то результат не совпадает с ожидаемым. Буду очень благодарен, если поможете мне найти ошибку в рассуждениях.
В общем, предположим
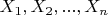
это i.i.d случайные величины с

и

.
Мы хотим найти предел распределения

где

при

.
Если прибавить еще

то получится новая случайная величина

такая, что

Обозначая

имеющую pdf

, получаем

Это можно упростить. Во первых,

, так что

. Во вторых,

имеет очень маленькую дисперсию

, поэтому вся почти масса ее распределения находится в окрестности 0. Так что интеграл будет ненулевым только для достаточно малых значений x. Поэтому можно разложить

.



и

, поэтому слагаемое с первой производной занулится после интегрирования, а слагаемое со второй производной будет порядка

. Также, нет смысла раскладывать внутри

и

если нужны только слагаемые больше, чем

. В общем, после интегрирования имеем


При

,

, поэтому умножив на

получаем диффур:

Если принять, что последнее слагаемое тоже зануляется, а также, что

, получим:



И это по сути ЦПТ. Пока все хорошо.
Но если обозначить

и рассмотреть ДУ со всеми слагаемыми, получим:


Можно попробовать искать решения в виде

Тогда имеем для разных порядков

:


И окончательно:

И тут возникает проблема. Если я вычислю

из уравнения порядка

(так как

), то

и

.
Но с другой стороны

и тогда

Если же я вычислю

и

из полного решения, я получаю

И тот факт, что

при

кажется совершенно неправильным.
Насколько я вижу, причина этих противоречий может быть в том, что множитель при

который я получил равен

, а не

. У меня есть несколько мыслей, как это можно поправить, но они какие-то неубедительные.
Например, один из способов получить "правильный" ответ это рассматривать не изначальный диффур, а



Тогда при

получаем уравнение

Его решение (при непрерывной p) с

после интегрирования от

до x соответствует неравенству Берри-Эссеена, а именно

где

это CDF

, а

это CDF нормального распределения.
Но я не знаю, почему я бы стал рассматривать вторые разности, не зная заранее ответа. И кажется, что третьи разности снова ведут к чему-то странному, так что это может быть просто совпадение.
В общем, вопрос в том, какие правильные шаги на этом пути и как их найти?



