Кажется, придумал. Рассмотрим кольцо
![$R = \mathbb Z[a_0, \ldots, a_n]$ $R = \mathbb Z[a_0, \ldots, a_n]$](https://dxdy-02.korotkov.co.uk/f/5/2/5/525a35563a44bc0b48542e684544232082.png)
всех многочленов от формальных коэффициентов

. В его локализации
![$R[a_0^{-1}]$ $R[a_0^{-1}]$](https://dxdy-01.korotkov.co.uk/f/c/8/f/c8f20e2fd21fa53ee94b129c70359bc782.png)
многочлен

имеет обратимый старший коэффициент, поэтому его дискриминант является точным квадратом по модулю 4. Это значит, что

в

для некоторого

и многочлена

. Так как мы возводим

в квадрат и берём по модулю

, сам многочлен

определён только по модулю

(как элемент
![$\mathbb F_2[a_0, \ldots, a_n]$ $\mathbb F_2[a_0, \ldots, a_n]$](https://dxdy-04.korotkov.co.uk/f/f/1/c/f1cc53753cdb9abfe7fe7fe6de45176c82.png)
), зато однозначно при фиксированном

. В случае

всё хорошо, так что предположим, что

. Кольцо
![$\mathbb F_2[a_0, \ldots, a_n]$ $\mathbb F_2[a_0, \ldots, a_n]$](https://dxdy-04.korotkov.co.uk/f/f/1/c/f1cc53753cdb9abfe7fe7fe6de45176c82.png)
является факториальным, в нём

делится на неприводимый элемент

. Если

, то это означает, что исходное сравнение можно сократить на

(так как

взаимно просто с 2 в факториальном кольце

). Если же
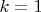
, то можно сократить на

и получить, что

. Это значит, что дискриминант обнуляется у всех многочленов над

с нулевым старшим членом. Но если взять конкретный неприводимый многочлен

над

степени ровно

, то у него дискриминант по формуле для многочленов

-й степени будет ненулевым: все корни такого формального многочлена - это корни

над алгебраическим замыканием

и ещё один корень на бесконечности, они попарно различны (или можно просто развернуть многочлен, если

, то получится разворот

, умноженный на

, у него все корни конечные и различны). Противоречие.



