n=2=3/2: 1/2=[2], len=1
n=3=11/6: 1/6=[6], len=1
n=4=25/12: 1/12=[12], len=1
n=5=137/60: 17/60=[4, 30], len=2
n=6=49/20: 9/20=[4, 5], len=2
n=7=363/140: 57/140=[3, 14, 420], len=3
n=8=761/280: 79/280=[4, 32, 1120], len=3
n=9=7129/2520: 431/2520=[6, 230, 57960], len=3
n=10=7381/2520: 179/2520=[15, 230, 57960], len=3
n=11=83711/27720: 551/27720=[56, 495], len=2
n=12=86021/27720: 2861/27720=[10, 312, 180180], len=3
n=13=1145993/360360: 64913/360360=[6, 75, 7480, 15315300], len=4
n=14=1171733/360360: 90653/360360=[4, 858, 2520], len=3
n=15=1195757/360360: 114677/360360=[4, 15, 858, 2520], len=4
n=16=2436559/720720: 274399/720720=[3, 22, 520, 55440], len=4
n=17=42142223/12252240: 6866737/12252240=[2, 17, 616, 1750320], len=4
n=18=14274301/4084080: 2062019/4084080=[2, 205, 72160, 66978912], len=4
n=19=275295799/77597520: 42503239/77597520=[2, 21, 8294, 24728880], len=4
n=20=55835135/15519504: 6242881/15519504=[3, 15, 444, 123728, 119629510], len=5
n=21=18858053/5173168: 1834619/5173168=[3, 47, 32080, 5152290, 1023565869340], len=5
n=22=19093197/5173168: 1599475/5173168=[4, 17, 2755, 4098960, 9608338319580], len=5
n=23=444316699/118982864: 31614757/118982864=[4, 64, 11979, 105365184, 27517925473038], len=5
n=24=1347822955/356948592: 79971413/356948592=[5, 42, 4305, 96155675, 961878294577200], len=5
n=25=34052522467/8923714800: 1642336733/8923714800=[6, 58, 7476, 67707640, 7669699600], len=5
n=26=34395742267/8923714800: 1299116933/8923714800=[7, 368, 173926, 19302383100], len=4
n=27=312536252003/80313433200: ?
n=28=315404588903/80313433200: 5849143897/80313433200=[14, 715, 559224, 70175996814, 2871270912355756419600], len=5
n=29=9227046511387/2329089562800: 89311739813/2329089562800=[27, 780, 36975, 14536368], len=4
n=30=9304682830147/2329089562800: 11675421053/2329089562800=[200, 77706, 16532874306, 59497349338165200], len=4




 , никогда не являются целыми.
, никогда не являются целыми. 


 до ближайших целых
до ближайших целых и
и 



 последовательность значений наименьших длин египетских дробей,
последовательность значений наименьших длин египетских дробей, . Мне удалось вычислить
. Мне удалось вычислить  :
:
 terms, one of the denominators is at most
terms, one of the denominators is at most  .
. from
from  to
to  ,
,  has an expansion with at most
has an expansion with at most  terms.
terms. - наименьшие длины обобщенных египетских дробей. Ясно, что
- наименьшие длины обобщенных египетских дробей. Ясно, что  , поэтому перебор не слишком сильно возрастает.
, поэтому перебор не слишком сильно возрастает. ?
? вместо отдельно округления вверх и вниз?
вместо отдельно округления вверх и вниз? вместо отдельно округления вверх и вниз?
вместо отдельно округления вверх и вниз?
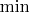 это отдельная тема.
это отдельная тема. 
![$[x,2x]$ $[x,2x]$](https://dxdy-01.korotkov.co.uk/f/4/0/6/406c23bde56c4683f77fe63cac3a0d6182.png) для некоторого
для некоторого  обычно сильно меньшего половины знаменателя.
обычно сильно меньшего половины знаменателя.
 .
. до
до  , а уже потом от
, а уже потом от  до
до  .
. можно сильно меньше: [1420599600, 2012868, 43, 90, 26].
можно сильно меньше: [1420599600, 2012868, 43, 90, 26]. - дробная часть гармонического числа, то из
- дробная часть гармонического числа, то из  следует
следует  , а из
, а из  следует
следует  - т.е. что можно проверять только округление к ближайшему.
- т.е. что можно проверять только округление к ближайшему. до
до  решений длины меньше 5 нет, а длина 5 перебирается очень долго.
решений длины меньше 5 нет, а длина 5 перебирается очень долго.

 - делитель
- делитель  , что
, что  и
и  делятся на
делятся на  . Но как его искать быстрее - непонятно.
. Но как его искать быстрее - непонятно.