2001650377515 3
2001650377515 = 1413065 * 1416531 ~ 0.0024528241800625405
2001650377516 = 1410334 * 1419274 ~ 0.00633892397120106
2001650377517 = 1408967 * 1420651 ~ 0.008292600181551535
2002361043967 3
2002361043967 = 1410319 * 1419793 ~ 0.006717629132132474
2002361043968 = 1392416 * 1438048 ~ 0.03277181531955975
2002361043969 = 1408563 * 1421563 ~ 0.00922926415076919
2002378206927 3
2002378206927 = 1412759 * 1417353 ~ 0.003251793122535318
2002378206928 = 1408804 * 1421332 ~ 0.008892649367832517
2002378206929 = 1413491 * 1416619 ~ 0.0022129606767924415
2002480835823 3
2002480835823 = 1412963 * 1417221 ~ 0.0030135254780203624
2002480835824 = 1400348 * 1429988 ~ 0.021166167266993607
2002480835825 = 1409131 * 1421075 ~ 0.008476145936751056
2002562418075 3
2002562418075 = 1412319 * 1417925 ~ 0.0039693581974045156
2002562418076 = 1413638 * 1416602 ~ 0.0020967178301658507
2002562418077 = 1412879 * 1417363 ~ 0.0031736617219166874
2002633882623 3
2002633882623 = 1411989 * 1418307 ~ 0.004474539107599318
2002633882624 = 1407008 * 1423328 ~ 0.011599081170824865
2002633882625 = 1413925 * 1416365 ~ 0.0017256926640381032
2002640420879 3
2002640420879 = 1413293 * 1417003 ~ 0.0026250749136944584
2002640420880 = 1406724 * 1423620 ~ 0.012010884864408267
2002640420881 = 1409279 * 1421039 ~ 0.00834469256974657
2002898596643 3
2002898596643 = 1415237 * 1415239 ~ 1.4131908647740943E-6
2002898596644 = 1415238 * 1415238 ~ 0.0
2002898596645 = 1409185 * 1421317 ~ 0.008609231577117349
2002966528643 3
2002966528643 = 1415261 * 1415263 ~ 1.413166899943974E-6
2002966528644 = 1415262 * 1415262 ~ 0.0
2002966528645 = 1411505 * 1419029 ~ 0.005330480586324571

 называется почтиквадратом, если его можно представить в виде произведения двух натуральных чисел
называется почтиквадратом, если его можно представить в виде произведения двух натуральных чисел , где
, где  и
и 
 .
. , так что при достаточно больших
, так что при достаточно больших  условие выполняется.
условие выполняется. . Тут тоже несложно, если
. Тут тоже несложно, если  то
то 
 , так чтобы
, так чтобы  , либо
, либо  разлагалось в произведение двух полиномов равной степени с равными старшими коэффициентами. Может поможете?
разлагалось в произведение двух полиномов равной степени с равными старшими коэффициентами. Может поможете?
 . Или, имеем уравнение Пелля
. Или, имеем уравнение Пелля  . Оно имеет бесконечно много решений, причем
. Оно имеет бесконечно много решений, причем 
 , а значит
, а значит 
 и далее квадрат по
и далее квадрат по 





 и т.д. Целые пятерки почтиквадратов ) Или Вам нужно
и т.д. Целые пятерки почтиквадратов ) Или Вам нужно 
 - почтиквадраты по определению. И таких
- почтиквадраты по определению. И таких  бесконечно много.
бесконечно много. после запятой в определении - суть ясна.
после запятой в определении - суть ясна. . Ничем не мудреней ряда Фибоначчи. Хорошее решение, но
. Ничем не мудреней ряда Фибоначчи. Хорошее решение, но 
 , а значит
, а значит
 выражение вправо стремится к
выражение вправо стремится к  , значит зажали между милиционерами.
, значит зажали между милиционерами. .
.

 - -решение, то
- -решение, то  - тоже решение.
- тоже решение. есть решение, то получаются бесконечно много, сколь угодно больших решений.
есть решение, то получаются бесконечно много, сколь угодно больших решений. Для каждой пары последовательных членов определены
Для каждой пары последовательных членов определены  и
и 




 и
и  — равенство треугольного и квадратного числа
— равенство треугольного и квадратного числа  Эту задачу в школе вполне могут знать:
Эту задачу в школе вполне могут знать:  и т.д. Если что, Серпинский на стр.
и т.д. Если что, Серпинский на стр.  показывает, как тут обойтись без Пелля.
показывает, как тут обойтись без Пелля. Тогда их целая пятерка:
Тогда их целая пятерка:



 , то есть числа вида
, то есть числа вида  , где
, где  . Тестировать числа на почтиквадратность по одному скорее всего медленно. Лучше тестировать все числа на некотором отрезке.
. Тестировать числа на почтиквадратность по одному скорее всего медленно. Лучше тестировать все числа на некотором отрезке.  , где
, где  и
и ![$x \in [a, b]$ $x \in [a, b]$](https://dxdy-02.korotkov.co.uk/f/d/e/e/dee96e9634467ae09910551cb84f284e82.png) , то
, то  ,
,  . Соответственно, для нахождения всех почтиквадратов на отрезке
. Соответственно, для нахождения всех почтиквадратов на отрезке ![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png) можно просто перебрать все такие пары
можно просто перебрать все такие пары 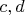 за линейное по
за линейное по  время.
время.![$[1, N]$ $[1, N]$](https://dxdy-01.korotkov.co.uk/f/4/7/1/471fe0fb120c88750aa8c050c0e2b6e182.png) . Если рассматривать множество произведений вида
. Если рассматривать множество произведений вида  для некоторой константы
для некоторой константы  . Но некоторые произведения будут задавать один и тот же почтиквадрат. Например, числа вида
. Но некоторые произведения будут задавать один и тот же почтиквадрат. Например, числа вида  , где
, где  - близкие друг к другу простые, допускают вплоть до шести различных подходящих разложений.
- близкие друг к другу простые, допускают вплоть до шести различных подходящих разложений. . Тогда все почтиквадраты в этом интервале будут иметь вид
. Тогда все почтиквадраты в этом интервале будут иметь вид  для некоторого натурального
для некоторого натурального  . Соответственно, для нахождения всех почтиквадратов достаточно перебрать все
. Соответственно, для нахождения всех почтиквадратов достаточно перебрать все  и дробь
и дробь  достаточно близка к 1.
достаточно близка к 1.