Note that I am working on a further improvement, but it is not ready yet.
I extended my Perl code to find solutions for
A309981, and then also extended the C code to do the same. To my surprise the Perl code was faster for about half the cases, and that appears to be because of an additional type of check it does. So I have added that to the C code.
It will add new options -c<n> ('check', default 0), -cp<n> ('check_prime', default 0), -cr<d> ('check_ratio', default 1.0), -cc<n> ('check_chunk', default 'check').
During initialization, it will analyse all moduli from 2 to 'check' (skipping moduli that are not 'check_prime'-smooth, if check_prime > 0) looking for modular values that are disallowed for the given chain. It will then combine the moduli into bitvectors of size at most 'check_chunk' bits, discarding any that do not have a reject ratio of at least 'check_ratio'. At runtime, during linear walk, we then do a single mod calculation and bitvector-lookup for each of those combined bitvectors aiming to reject a value before doing any further primality or factorization tests. Obviously if only one value remains allowed for a particular modulus, we handle that directly.
The 3 types of constraint are pretty simple: 1) for a modulus m and target divisors t, if
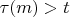
then no value in the chain can be a multiple of m, and if
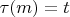
then no value
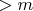
can be; 2) writing
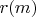
for rad(m): if
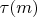
does not divide t then
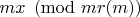
is disallowed for each x coprime with
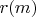
; 3) if a square is fixed at some value, then quadratic non-residues
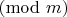
are disallowed.
Some experimentation will be required to find optimal values for the 4 new options; I believe that a speedup of between x 2 and x 10 is realistic, but it is likely to vary a lot for specific values.