Забывая о выпуклости

(не могу сообразить, как это может быть),
если

это функция распределения, то мысль идёт в направлении того, чтобы сделать

. Тогда p в Бернулли будут соответствовать её квантилям, поэтому мы смогли бы "взвесить" для Z функцию плотности вероятности от X

его же функцией распределения

.
Если для

взять самую удобную функцию распределения (стандартное логистическое распредление с
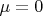
и

), то получаем:

и, нормализуя её интегралом

, получаем функцию плотности вероятности

и функцию распределения соответственно

. Это как частный случай.
Ничего не напутал?
Симуляция в Питоне подтверждает, что аналитически для данного частного случая оно так:
import numpy as np
from scipy.stats import logistic, ks_1samp
размер_выборки_MC = 100000
rv = logistic(loc=0, scale=1)
X = rv.rvs(size=размер_выборки_MC)
p = rv.cdf(X)
Y = np.random.binomial(1, p=p)
Z = X[Y.astype(bool)]
target_pdf = lambda x: 2.0 * np.exp(-x) / np.power(1 + np.exp(-x), 3)
target_cdf = lambda x: -2.0 / (np.exp(x) + 1) + 1.0 / np.power(np.exp(x) + 1, 2) + 1
ks_1samp(Z, target_cdf)
Просветите, пожалуйста, что это значит.
Просто подчеркивание зависимости события

от значения

.