Уравнение в рациональных числах

[Trueman]

Пусть $l,p\in \mathbb Q$ Вопрос - всегда ли уравнение

$$\frac{{l}}{{x^2}}+x^2-p=y^2$$

разрешимо в рациональных числах и если разрешимо, то сколько решений имеет ?

[Руст]

Это эллиптическое уравнение. Всегда можно перейти с помощью дробно линейных преобразований к стандартной форме. Считать ранг кривой (над Q) и узнать как устроено множество решений (бесконечно или конечно). Надеюсь несколько знакомы с эллиптическими кривыми (например по книжке Прасолова), тогда сами всё можете выяснить.

[maxal]

Trueman писал(а):

Пусть $l,p\in \mathbb Q$ Вопрос - всегда ли уравнение

$$\frac{{l}}{{x^2}}+x^2-p=y^2$$

разрешимо в рациональных числах и если разрешимо, то сколько решений имеет ?

Можно начать с элементарного сведения к эллиптическому уравнению 3-й степени.
Исходное уравнение эквивалентно:

$$4l - p^2 + (2x^2 - p)^2 = (2xy)^2$$

или

$$4l - p^2 = (2xy+2x^2 - p)(2xy-2x^2 + p),$$

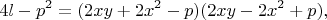
все решения которого находятся из разложения числа $4l - p^2$ в произведение двух рациональных множителей $a,b$:

$$\begin{cases} 4l - p^2 = a\cdot b\\ a - b + 2p = 4x^2\\ a+b = 4xy \end{cases}$$

Понятно, что последнее уравнение однозначно определяет $y$ и про него можно на время забыть; а вот второму уравнению удовлетворяет не всякая пара $(a,b)$. В купе с первым уравнением оно приводит к эллиптическому уравнению 3-й степени:

$$(a+p)^2 - 4l = 4ax^2$$

которое уже дальше можно можно приводить к стандартной форму и решать (относительно $a,x$) как написал Руст.

К сожалению, без конкретных значений $l,p$ здесь вряд ли можно сказать что-то большее.