С чего вдруг? Линия тока показывает только направление скорости, а ее величина вдоль такой линии может меняться как угодно. Пример - расширяющаяся труба.
В этом примере труба не расширяющаяся, а постоянного сечения. А для того, чтоб скорость

в линиях тока изменилась в прямой трубе, необходимо чтоб эти линии тока начали изгибаться, т.е. появились радиальные компоненты скорости
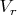
, в чем я сомневался.
Цитата:
Остальное я не понял, но складывается впечатление, что Вы считаете, что вся энергия жидкости сидит в ее кинетической энергии. Это не так. Кроме кинетической энергии есть еще давление, выполняющее роль потенциальной энергии (тот же пример с расширяющейся трубой - скорость падает, давление растет).
Жаль, что не поняли. Наверное коряво объяснил. Я как раз рассматриваю давление как потенциальную функцию. Попробую еще раз:
1) Есть резервуар с повышенным давлением постоянного значения

. Будем считать его емкость бесконечной. Из него вода подается в трубу, через две трубки малых диаметров, по касательной, в проекции перпендикулярно оси Y. Линии тока вначале идут примерно как показано на рисунке, затем выпрямляются.
Силы, которые действуют на элементы жидкости, пока линии тока не выпрямились, раскладываются на центростремительные, и действующие вдоль оси Y, и могут быть описаны как:

Момент этих сил равен нулю, поэтому
сохраняется момент импульса, с которым жидкость выходит из малых трубок в большую трубу, его модуль:

, откуда имеем:

Далее, для удобства рассматриваю проекции сил, которые фигурируют в (1а), на радиус-вектор и на ось y, и соответствующие им проекции ускорений единицы объема жидкости (уравнения Эйлера):

После выпрямления линий тока, уравнения (3а) принимают вид:

.
2). Далее, рассматривается только участок с параллельными оси y линиями тока. Как раз, в связи с тем, что давление является потенциальной функцией, на рассматриваемом участке оно определится как

Это, собственно уравнение Бернулли. Перегруппируйте его члены,
и получите приращение кинетической энергии, как убыли потенциалов (давления). А вы говорите, я не учитывал потенциальной энергии. При этом угловая скорость зависит от радиуса, и определяется выражением (2а). А скорость

одинакова во всех линиях тока, и не изменяется вдоль y.
3). Поставили винт (после участка с параллельными линиями тока). Теперь жидкость на участке с винтом "скользит" вдоль винтовой поверхности со скоростью

. Или я не прав в этом месте?
Согласно (6а) скорости

теперь разные и зависят от радиуса (поскольку

зависит от радиуса). В пределах линии тока

одинакова (потому-что по условию линии тока параллельны оси y, в трубе постоянного сечения).Согласно (5а) распределение давлений в линиях тока тоже другое, из-за разных скоростей

. И если до установки винта, оно отвечало 4(а), то после
установки, в связи с изменением распределения давления, оно должно принять общий вид (3a). Т.е. должна появляется радиальная составляющая
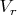
. А по условию ее нет - линии тока прямые.
И в этом мне показалось противоречие, для разрешения которого надо принять, что давление в линиях тока остается таким же как до установки винта, не смотря на изменение

, и уравнение (3а) имеет вид (4а). Тогда всплыл бы вопрос о несохранении энергии (с учетом потенциальной энергии давления).
4). И тут можно возразить - "Почему бы линиям тока не искривляться вблизи винта таким образом, чтоб перераспределение давлений и скоростей удовлетворяло закону сохранения энергии, при этом на участке с прямыми линиями тока была такая же картина, как и до установки винта? Почему я вдруг решил,
что линии тока везде прямые, и не искривляются?" Ну, я думал потому, что в этом случае на участке с винтом они должны были бы сгущаться, или ближе к оси трубы, или к максимальному радиусу. Это означало бы опять наличие распределения

вдоль радиуса и появлению радиальной составляющей скорости, только уже на винтовом участке. И это показалось не правдоподобным. Хотя сейчас
есть версия, что жидкость просто огибает место стыка винта с трубой. А потом, после стыка, скорость

во всем сечении винта становится одинаковой, как и до стыка. Все равно не правдоподобно...,т.к. и угловая скорость должна была бы стать одинаковой по линиям тока на винтовом участке (если принять справедливым соотношение (6а)).