Добрый день !
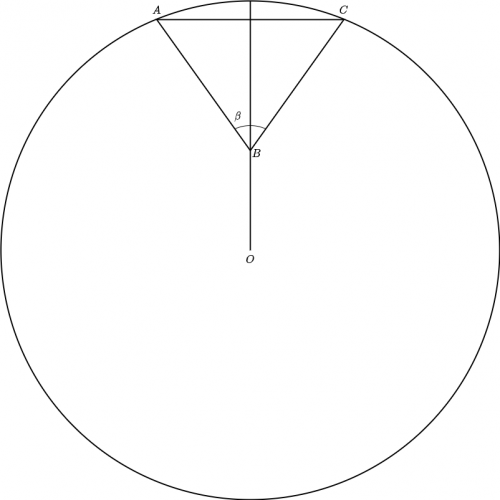
Прошу помощи в решении прикладной задачи. Имеется окружность с центром

радиусом

и равнобедренный треугольник

. Вершины

и

лежат на окружности, а вершина

лежит на радиусе. Расстояние

и угол

при вершине

известны. Требуется найти

.
Что мне понятно в такой постановке задачи:
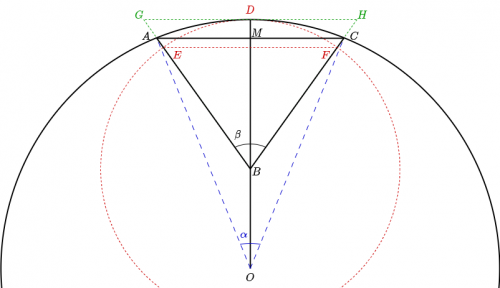
Можно вычислить расстояние

. Отсюда можно определить

и

.
Треугольники

и

полностью решены. Искомая хорда находится в диапазоне

Искомую хорду

можно выразить через центральный угол

но угол

не известен.
Можно рассмотреть эллипс с фокусами

и

. У него известен один фокальный радиус

и угол между вторым фокальным радиусом

и большой полуосью равный

. В этом случае нужно определить либо значение фокального радиуса

, либо угол

либо расстояние

от точки

до большой полуоси эллипса.
Еще я пробовал решить систему уравнений для нахождения координат точки


пересечения окружности и отрезка

