Недавно узнал о
парадоксе Бертрана и возникли некоторые вопросы.
Напомню, что парадокс Бертрана заключается в следующем. Имеется равносторонний треугольник, вписанный в окружность. Случайным образом выбирается хорда окружности. Какова вероятность, что выбранная хорда окажется длиннее стороны треугольника? Жозеф Бертран предложил три разных способа решения этой задачи, каждый из которых выглядит очевидно верным, но при этом получаются очень разные результаты. В этом и состоит парадокс.
Возможно, я чего-то не понимаю, но как по мне, объясняется этот парадокс элементарно:
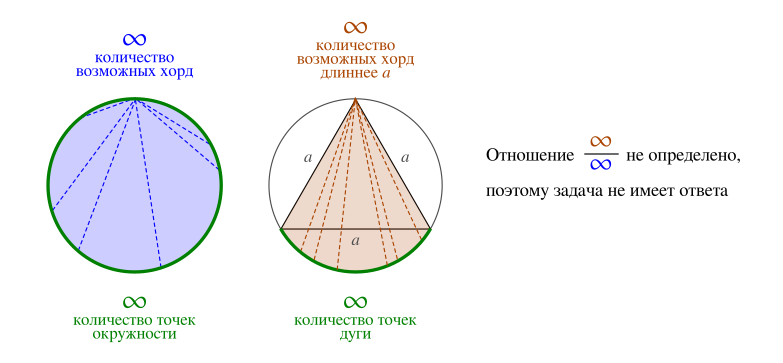
1. Окружность содержит бесконечное количество точек. Поэтому из любой точки окружности можно провести
бесконечное количество хорд к остальным точкам.
2. Дуга окружности размером в треть этой окружности также содержит бесконечное количество точек. Поэтому из вершины равностороннего треугольника можно провести
бесконечное количество хорд, имеющих общую точку с данной дугой, и при этом отвечающих требованию быть длиннее стороны вписанного равностороннего треугольника.
3. Как итог, получаем отношение

, т.е.
неопределённость. (Насколько мне известно, в математике результат деления бесконечности на бесконечность не определён.)
Вот и весь внутренний механизм парадокса. Мы получаем противоречивые ответы, зависящие от способа решения, просто потому, что результат на самом деле не определён.
Конечно, как и всегда в ситуации, когда "ларчик слишком просто открывался", сразу возникает подозрение, что я чего-то упускаю из виду. Ведь не могла же куча умных людей, ломавших голову над этим парадоксом до меня, пройти мимо такого очевидного и банального объяснения ситуации?.. А тут вдруг явился я, почти ничего не понимающий в математике, "немного покумекал" и сразу всё понял?.. Обычно такое бывает только в очень наивных мечтаниях.
Но как я ни старался, у меня не получается найти изъяны в своей логике. Также я не нашёл в сети никаких попыток рассуждать схожим образом (может, не там искал). Выходит, то ли моё объяснение парадокса Бертрана слишком тупое, и люди стесняются даже озвучивать такие мысли, то ли наоборот, идея слишком гениальная. :) Может, кто-нибудь подскажет, что я делаю не так?
А теперь самое интересное. В процессе мучительных размышлений над парадоксом непонимания людьми этого парадокса, когда я пытался поэтапно проверить свой метод рассуждений, мне пришёл в голову собственный маленький симпатичный парадокс и окончательно доломал мой мозг.
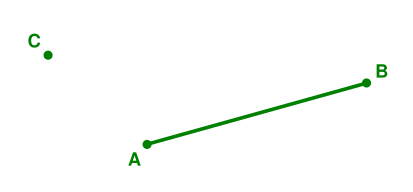
Простая задачка. Имеется отрезок

и точка

, не лежащая на прямой

. Какова вероятность того, что случайная прямая, проведённая через точку

, пересечёт отрезок

(будет иметь с ним общую точку)?
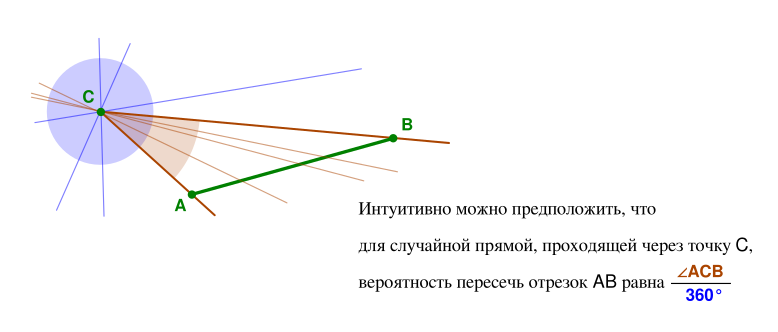
По идее, ответ достаточно очевиден, отношение

будет искомой вероятностью:
Но вот если применить мой предыдущий метод рассуждений, то начинаются чудеса:
1. Прямая, заданная отрезком

, содержит бесконечное количество точек. Значит, через точку

можно провести
бесконечное количество прямых, пересекающих прямую

(а также можно ещё провести одну прямую, параллельную

).
2. Отрезок

также содержит бесконечное количество точек. Значит, через точку

можно провести
бесконечное количество прямых, имеющих общую точку с отрезком

.
3. Искомый результат, по идее, должен быть отношением количества точек отрезка

к общему количеству точек прямой, на которой он лежит. (Если совсем точно, то делим на

, поскольку есть ещё вариант, когда через точку

можно провести прямую, параллельную отрезку

, но это в данном случае ни на что не влияет, ведь

это по-прежнему

.) Соответственно, опять получаем отношение

, т.е.
неопределённость.
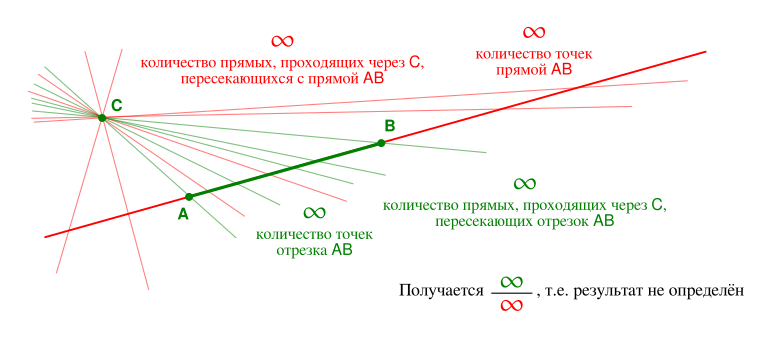
Вот и получается парадокс. Ответ зависит от способа решения, как и в случае с парадоксом Бертрана, и в целом эта задачка выглядит родственной ему.
И как с этим быть? Если такой способ рассуждений приводит к странному результату, значит, он некорректен?.. Но что именно с ним не так? Я не понимаю. Вроде ведь всё логично?
Обычно, если в ходе рассуждений получаешь бред, и при этом изъянов в логике нет, это означает, что не верны исходные данные (так, к примеру, работает доказательство от противного). Но что может быть неверным в данном случае? Или всё правильно, и задачка действительно не имеет решения, а интуитивно очевидный вариант решения ложен?
Или одно другому не мешает, и верны оба варианта решения моей задачки?.. Ведь неопределённость ответа означает, что он может быть любым, в том числе и

.
В общем, мои мозги с этим не справляются. Может, кто умный подскажет, можно ли так в целом рассуждать (а если нельзя, то почему), и что всё это значит в итоге?