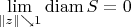Пусть

-- равномерно выпуклое нормированное пространство.
Напомним, что нормированное пространство называется равномерно выпуклым если для любого

найдется

такое, что

В точке

находится источник света. Доказать, что при приближении источника к шару

, диаметр светового пятна на поверхности шара стремится к нулю.
-- 26.01.2023, 17:11 --Чуть более формально,

-- световое пятно на единичном шаре. Доказать: