It's easy to show that there must be at least one pair
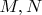
.
We just start with first point
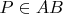
, then built the bisector
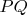
of
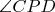
, and after that the director
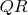
of
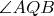
.
Since

is inscribed , thus convex,

is always lying between

and

. It means that if
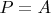
, the point

is between

and

, and if
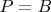
-- between

and

.
While

is moving continuously, so is

, and at some point they cross, which means that
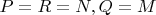
. So existence is proven.
But.
This approach doesn't help us to prove uniqueness. Surely, we can introduce a variable
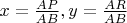
, define closed form for a function
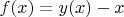
and prove that

is monotonous, or
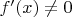
if
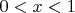
. Though, it's incredibly hard.
Next attempt is geometry...