√m≈√x+√y

[juna]

Реализовал пока алгоритм $x^2\equiv R\mod p$ по простому модулю. Заявленная вычислительная сложность $O(\log^4(p))$. Считает мгновенно на числах большой разрядности.

/* solve x^2=a mod p, p is prime */
modulop(a,p):=block([h, N1, N2,jacob, N,a1,a2, k,p1,j,i, b, c, d, ji],
  if primep(p) then
    block(
             jacob: jacobi (p, a),
        if jacob = -1 then
          "No solutions"
        else
          block(
             h:p-1,
        k:0,
        while mod(h,2)=0 do block(h:h/2,k:k+1),
             N:5,
        while jacobi (p, N)=1 do N:N+1,
        a1:power_mod(a, (h+1)/2,p),
        N1:power_mod(N,h,p),
        N2:1, j:0, a2:inv_mod(a,p),
        for i:0 thru k-2 do
          block(
                    b:mod(a1*N2,p), c:mod(a2*b^2,p),
               d:power_mod(c,2^(k-2-i),p),
               if d = 1 then ji:0,
               if d=p-1 then ji:1,
               N2:mod(N2*power_mod(N1,(2^i*ji),p),p)
                  ),
      [mod(a1*N2,p), p-mod(a1*N2,p)]
                   )
        )
  else
    "Not prime"
    )$
modulop(87,101);

Воспользоваться можно через любой online сервис, например http://maxima.cesga.es/

Вставляем вышеуказанный код, в функцию modulop подставляем нужные a и p (правда в online версии символ Якоби как-то для длинных простых плохо считается, поэтому все-таки лучше оффлайн последняя версия maxima).

-- Ср янв 11, 2023 22:48:28 --

(Оффтоп)

Утундрий в сообщении #1576796 писал(а):

Надо будет на досуге и себе завести птичью тему. Что-нибудь вроде разложения кубического корня свободного от кубов целого числа на сумму трёх квадратных корней свободных от квадратов целых чисел.

И у Вас по заявленному вопросу есть какой-то задел? В противном случае содержательное общение можно продолжить только в пургатории...

[Andrey A]

juna
Я пока свои тупички не обойду, не уймусь, на будущее очень интересно. Но кое что по горячим следам. Положим, нам не известно простое $m$ или составное. Берем произвольный квадрат (или "неудобный" для процедуры, если такое возможно), делим его на $m$, получаем вычет $R$. Запускаем процедуру по $R$ и получаем другой, удобный ей квадрат. Программе ничего не известно о природе $m$, но мы получили пару сравнимых квадратов и можем делать выводы о делимости. Если процедура быстрее известных методов факторизации, нет ли в том противоречия? А что если $R$ — целый квадрат. Влияет это на ее поведение?
На alpertron.com помните как было — программа делает массу только ей нужных вещей, все по уму и очень солидно, а в самом корне сидит маленький такой переборчик.

[juna]

Andrey A в сообщении #1576830 писал(а):

Если процедура быстрее известных методов факторизации, нет ли в том противоречия?

Конечно, конкретно эта процедура не быстрее алгоритма проверки на простоту (для больших $p$ там, по-моему, вероятностный тест Миллера-Рабина запускается). В функции modulop первой же строчкой идет:

if primep(p) then

Заявленная вычислительная сложность получается, после того, как проверили, что число простое, тоже самое будет для составных $m$ - первым делом пойдет их факторизация.

Andrey A в сообщении #1576830 писал(а):

программа делает массу только ей нужных вещей, все по уму и очень солидно, а в самом корне сидит маленький такой переборчик.

Конкретно здесь переборчика всего 3, не считая всяких внутренних power_mod (модульное возведение в степень), inv_mod(мультипликативно обратное):

      h:p-1,
        k:0,
        while mod(h,2)=0 do block(h:h/2,k:k+1),

Находим степень двойки в p-1.

N:5,
        while jacobi (p, N)=1 do N:N+1,

Находим первый попавшийся квадратичный невычет.

for i:0 thru k-2 do

Цикл по количеству найденных ранее 2 в p-1. Отсюда, в частности, понятно, что худшие случаи для алгоритма - это простые числа вида $p=2^n+1$

[Andrey A]

Ага. Тест на простоту как базовая операция. И квадраты не только по $R$, но и по всем нужным вычетам (двойку-то зря что-ли в $ (p-1)$ возводили?). Отлично. Осталось подставить всё это в известные нам формулы, упорядочить по величине погрешности, и... вот оно решение. Которое всё равно захочется проверить перебором, мало ли... ) Ведь захочется? По двойке тоже есть свои квазипростые. Знаете что, мне Ваши исследования интересны, по ссылкам буду еще разбираться, но если честно — много ли радости в таком решении? Вроде как древнюю перебор-пушку меняем на современные ПЗРК. Всё по тем же воробьям. Нет. Всё-таки хочется прямой алгоритм.

[juna]

Улучшил предыдущий код:

/* solve x^2=a mod p, p is prime */
modulop(a,p):=block([h, N1, N2, legandr, N,a1,a2, k,p1,i, b, c, d, j],
  if primep(p) then
    block(
             legandr: power_mod(a,(p-1)/2,p),
        if legandr = p-1 then
          "No solutions"
        else
          block(
             h:p-1, k:0,
        while mod(h,2)=0 do block(h:h/2,k:k+1),
             N:2,
        while power_mod(N,(p-1)/2,p)=1 do N:N+1,
        a1:power_mod(a, (h+1)/2,p), N1:power_mod(N,h,p),
        N2:1, j:0, a2:inv_mod(a,p),
        for i:0 thru k-2 do
          block(
                    b:mod(a1*N2,p), c:mod(a2*b^2,p),
               d:power_mod(c,2^(k-2-i),p),
               if d = 1 then j:0,
               if d=p-1 then j:1,
               N2:mod(N2*power_mod(N1,(2^i*j),p),p)),
           j:mod(a1*N2,p),
      [j, p-j]))
  else
    "Not prime")$

Реализовал нахождение решения сравнения $v^2\equiv R\mod m$ для $m=p_1\cdot p_2$:

/* solve x^2=a mod m, m = p1 * p2 */
modulop1p2(a,m):= block([fact:ifactors(m), ans1, ans2,res:[]],
  if length(fact) # 2 then
   "m is not equal p1*p2"
  else
    block(
      if (fact[1][2] = 1) and (fact[2][2] = 1) then
      block(
        ans1:modulop(a,fact[1][1]),
        ans2:modulop(a,fact[2][1]),
        res:cons(chinese([ans1[1],ans2[1]],[fact[1][1], fact[2][1]]), res),
        res:cons(chinese([ans1[1],ans2[2]],[fact[1][1], fact[2][1]]), res),
        res:cons(chinese([ans1[2],ans2[1]],[fact[1][1], fact[2][1]]), res),
        res:cons(chinese([ans1[2],ans2[2]],[fact[1][1], fact[2][1]]), res),
        res)
      else
        "m is equal p1^a*p2^b, a or b > 1" ))$

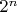
Для общего вида $m$ больно муторно перебирать все $2^n$ комбинаций, где $n$ - число простых делителей $m$.

Для эффективного перебора нужно еще разработать правила останова для $R$.

Пусть известно решение $v_1^2\equiv R_1\mod m$, найдем ограничение для $R_2, v_2$, для которых возможно лучшее приближение.

Имеем:

$$2m-\sqrt{(m-v_1)^2-R_1}-\sqrt{(m+v_1)^2-R_1}>2m-\sqrt{(m-v_2)^2-R_2}-\sqrt{(m+v_2)^2-R_2}$$

т.е. должно выполняться:

$$\sqrt{(m-v_1)^2-R_1}+\sqrt{(m+v_1)^2-R_1}<\sqrt{(m-v_2)^2-R_2}+\sqrt{(m+v_2)^2-R_2}$$

Обозначим $a=\sqrt{(m-v_1)^2-R_1}+\sqrt{(m+v_1)^2-R_1}, b=(m-v_2)^2, c=(m+v_2)^2$

Возводим в квадрат:

$$a^2<b-R_2+c-R_2+2\sqrt{(b-R_2)(c-R_2)}$$

$$a^2-b-c+2R_2<2\sqrt{(b-R_2)(c-R_2)}$$

Возводим еще раз в квадрат:

$$(a^2-b-c+2R_2)^2<4(b-R_2)(c-R_2)$$

$$(a^2-b-c)^2+4R_2(a^2-b-c)+4R_2^2<4bc-4bR_2-4cR_2+4R_2^2$$

$$(a^2-b-c)^2+4R_2a^2<4bc$$

$$R_2<\frac{4bc-(a^2-b-c)^2}{4a^2}$$

После всех подстановок и сокращений окончательно получаем (если не ошибся):

$$R_2<m^2-\frac{a^2}{4}+v_2^2-\frac{4m^2v_2^2}{a^2}$$

Поскольку $4m^2>a^2$, то функция $f(v_2)=v_2^2(1-\frac{4m^2}{a^2})$ достигает максимума в точке $v_2=0$.

Поэтому имеем следующее ограничение:

$$R_2<m^2-\frac{a^2}{4}$$

Но это не особенно полезно.

$$v_2<\sqrt{\frac{m^2-\frac{a^2}{4}-R_2}{\frac{4m^2}{a^2}-1}}$$

А вот на это можно опираться. Для этого добавим еще порцию кода:

delta(m,R,L):=block([dd,v,vv,i:1,j],
  while not(integerp(xy(m,L[i],R)[1])) and (i<length(L)) do i:i+1,
  dd:bfloat(2*m-sqrt((m-L[i])^2-R)-sqrt((m+L[i])^2-R)),vv:L[i],
  for j:i+1 thru length(L) do
    block(
    if (dd>bfloat(2*m-sqrt((m-L[j])^2-R)-sqrt((m+L[j])^2-R))) and (integerp(xy(m,L[j],R)[1])) then
      block(dd:bfloat(2*m-sqrt((m-L[j])^2-R)-sqrt((m+L[j])^2-R)),vv:L[j])),
  if integerp(xy(m,vv,R)[1]) then
  [vv,dd]
  else
  false)$
xy(m,v,R):=([((m-v)^2-R)/(4*m),((m+v)^2-R)/(4*m)])$
fpprec:30$
v2(m,v1,R1,R2):=block([a], a:bfloat(sqrt((m-v1)^2-R1)+sqrt((m+v1)^2-R1)),bfloat(sqrt((m^2-a^2/4-R2)/(4*m^2/a^2-1))))$

Функция delta(m,R,L) выбирает из списка L решений сравнения $v^2\equiv R\mod m$ целочисленное решение с минимальной ошибкой $2m-a$, если целочисленных решений нет, то возвращается false.

Функция xy(m,v,R) просто получает список решений $x,y$ для заданных $m,v,R$.

Функция v2(m,v1,R1,R2) считает собственно верхнее ограничение для $v_2$ по полученной формуле для известных $v_1,R_1$ и нового $R_2$.

Продемонстрируем на примере треугольного числа (максимального в указанной ранее таблице) $m=714195944281=597577\cdot 1195153$

(%i7) delta(714195944281,1, modulop1p2(1, 714195944281));
(%o7)         [714193553974, 2.09178501637662800360928372356b-7]
(%i8) v2(714195944281, 714193553974, 1, 2);
(%o8)                 7.14191163658994066022843741247b11
(%i9) delta(714195944281,2, modulop1p2(2, 714195944281));
(%o9)                                false
(%i10) v2(714195944281, 714193553974, 1, 3);
(%o10)                7.14188773335993878063157787733b11
(%i11) delta(714195944281,3, modulop1p2(3, 714195944281));
(%o11)                               false
(%i12) v2(714195944281, 714193553974, 1, 4);
(%o12)                7.14186383004993475900066029253b11
(%i13) delta(714195944281,4, modulop1p2(4, 714195944281));
(%o13)        [714191163667, 4.18357703366352418061779872005b-7]
(%i14) v2(714195944281, 714191163667, 4, 5);
(%o14)                7.14189968508510919964289242979b11
(%i15) delta(714195944281,5, modulop1p2(5, 714195944281));
(%o15)                               false
(%i16) v2(714195944281, 714191163667, 4, 6);
(%o16)                7.14188773348010840036651324299b11
(%i17) delta(714195944281,6, modulop1p2(6, 714195944281));
(%o17)                               false
(%i18) v2(714195944281, 714191163667, 4, 7);
(%o18)                7.14187578185510713252166124388b11
(%i19) delta(714195944281,7, modulop1p2(7, 714195944281));
(%o19)                               false
(%i20) v2(714195944281, 714191163667, 4, 8);
(%o20)                7.14186383021010529569837096844b11
(%i21) delta(714195944281,8, modulop1p2(8, 714195944281));
(%o21)        [214899754753, 1.23165381973183718500308714283b-11]
(%i22) v2(714195944281, 214899754753, 8, 9);
(%o22)               1.08650074855601945444046486567b11 %i

Итак, на $R=8$ уперлись. Имеем в порядке убывания точности:

$$\sqrt{714195944281}\approx\sqrt{87264806974}+\sqrt{302164561727}, R=8$$

$$\sqrt{714195944281}\approx\sqrt{2}+\sqrt{714193553976}, R=1$$

$$\sqrt{714195944281}\approx\sqrt{8}+\sqrt{714191163675}, R=4$$

(%i33) bfloat(sqrt(714195944281));
(%o33)                 8.45101144408762471059270771886b5
(%i34) bfloat(sqrt(87264806974)+sqrt(302164561727));
(%o34)                 8.45101144408762471059263484866b5
(%i35) bfloat(sqrt(2)+sqrt(714193553976));
(%o35)                 8.45101144408762470935511324262b5
(%i36) bfloat(sqrt(8)+sqrt(714191163675));
(%o36)                 8.45101144408762470811751462432b5

-- Вс янв 15, 2023 17:12:19 --

Andrey A в сообщении #1576869 писал(а):

много ли радости в таком решении

Для составных общего вида радости немного, поскольку там наблюдается экспоненциальный рост от количества простых делителей, плюс факторизация нужна.

На алгоритм, который я реализовал в виде функции modulop, оказывается указывал еще waxtep:

waxtep в сообщении #1570810 писал(а):

Тогда, для простого $m$, можно попробовать перебирать значения $R$ по возрастанию (причем, не все $R$ будут разрешены по соображениям взаимности) и в лоб извлекать из них корни по модулю $m$, - здесь же есть быстрые алгоритмы (не имел реального опыта реализации, но вот пишут: Алгоритм Тонелли—Шенкса
; есть некоторые оговорки, но, на первый взгляд, алгоритм не выглядит устрашающим/безнадежным).

https://ru.wikipedia.org/wiki/%D0%90%D0 ... 1%81%D0%B0

[Andrey A]

juna
Я насчет "против лома нет приема" был неправ, конечно. Есть методы, и у Давенпорта кое-что описано, но они либо не элементарны, либо предполагают знание квадрата по единице и т.д. Боюсь, мы тут ставим телегу впереди лошади, и задача в таком виде теряет привлекательность. У меня тут еще одна химера рухнула, не стал и выкладывать. Знаете, я, пожалуй, возьму паузу. Надо успокоиться, заодно и в Ваших выкладках поразбераюсь. От такого беспрерывного бодания добра не жди, иногда нужно отвлечься или просто отдохнуть.

[juna]

Andrey A в сообщении #1577225 писал(а):

От такого беспрерывного бодания добра не жди, иногда нужно отвлечься или просто отдохнуть.

На мой взгляд имело место обычное критическое осмысление фактов...
Кстати, думаю, для простых $m$, аналог подхода Тонелли—Шенкса может существовать и в интерпретации цепных дробей, но уровень требуемого инсайта там наверное потребует 10 дана.

[juna]

И все-таки оценка

$$R_2(m,v_1, R_1)\leq\left\lfloor m^2-\frac{\left(\sqrt{(m-v_1)^2-R_1}+\sqrt{(m+v_1)^2-R_1}\right)^2}{4}\right\rfloor$$

довольна удобна для нахождения новых ограничений на $R_2$ и можно пользоваться только ей.
Продемонстрирую на паре примеров треугольных чисел (хотя она справедлива для любых чисел).

$m=12403$

Мы начинаем с $R_1=1$ находим $v_1=12088, \delta=1.6e-3$, тогда $R_2(12403,12088,1)\leq 19$.

-- Чт янв 19, 2023 08:45:50 --

Берем $R_1=2$, нет решений
Берем $R_1=3$, нет решений
Берем $R_1=4$, находим $v_1=11773, \delta=3.26e-3$, поскольку погрешность больше, оставляем старое ограничение.
Берем $R_1=5$, нет решений
Берем $R_1=6$, нет решений
Берем $R_1=7$, нет решений
Берем $R_1=8$, нет решений
Берем $R_1=9$, находим $v_1=11458, \delta=4.95e-3$, поскольку погрешность больше, оставляем старое ограничение.
Берем $R_1=10$, нет решений
Берем $R_1=11$, нет решений
Берем $R_1=12$, нет решений

-- Чт янв 19, 2023 08:52:29 --

Берем $R_1=13$, находим $v_1=4060, \delta=1.17e-3$, поскольку погрешность оказалась меньше, обновляем ограничение $R_2(12403, 4060, 13)\leq 14$
Берем $R_1=14$, нет решений
Таким образом, процесс закончен на $R=13$.

$m=1891$

Опять начинаем с $R_1=1$ находим $v_1=1768, \delta=4.2e-3$, тогда $R_2(1891,1768,1)\leq 7$.
Берем $R_1=2$, нет решений
Берем $R_1=3$, нет решений
Берем $R_1=4$, находим $v_1=1645, \delta=8.69e-3$, поскольку погрешность больше, оставляем старое ограничение
Берем $R_1=5$, находим $v_1=1246, \delta=4.67e-3$, поскольку погрешность больше, оставляем старое ограничение
Берем $R_1=6$, нет решений
Берем $R_1=7$, нет решений
Таким образом, остается $R=1$.

[Andrey A]

juna
Хорошо, да больно хлопотно. И зачем проверять всё подряд? Вы же сами открыли чудесную последовательность A003658.

[juna]

Andrey A в сообщении #1577885 писал(а):

И зачем проверять всё подряд? Вы же сами открыли чудесную последовательность A003658
.

Программе она неизвестна (а заморачиваться, как-то ее генерить - ленно), да и если ставить вопрос не только о лучшем приближении, нужно рассматривать все $R$.

[Andrey A]

juna в сообщении #1577889 писал(а):

нужно рассматривать все $R$.

Лучшее — всегда приведенное. Последовательность свободных от квадратов программе известна? Просто домножить ее на $4$ кроме $4k+1$-ых членов.

[juna]

Andrey A в сообщении #1577895 писал(а):

Последовательность свободных от квадратов программе известна?

Нет, конечно. Для реализации нужно факторизацией $R$ заниматься, маленьких правда, но кто знает.

Я вот думаю о попеременном уточнении $R$ через $v$ и обратно.

[juna]

Проверил все треугольные, представимые произведением двух простых в пределах доступных нам таблиц
Максимальное $m$ с $R=1$ - это $m=25651$, дальше уже действительно нет ни одного.
Максимальное $R=92$ для $m=25239989503$.

Вот код программки с учетом разработанного ранее:

sqrtmm(m):=block([Rm,dm,vm,R1,v1,d,RR2, dd,xx],
   R1:1,dd:delta(m,R1,modulop1p2(R1,m)),
   d:dd[2],v1:dd[1],
   Rm:R1, dm:d,
   vm:v1,RR2:R2(m,v1,R1),
   while R1<RR2 do 
     block(
       R1:R1+1,
       dd:delta(m,R1,modulop1p2(R1,m)),
       if dd # false then
         block(
         d:dd[2],v1:dd[1],
         if d<dm then
           block(
             Rm:R1, dm:d, vm:v1,RR2:R2(m,v1,R1)))),
   xx:xy(m,vm,Rm),
   [m,dm,Rm,vm,xx[1],xx[2]])$

[Andrey A]

Пишу после перерыва. Вкратце. Вопрос существования иррациональности вида $\sqrt{a}+\sqrt{b}$ на заданном интервале оказывается сложнее, чем выглядит на первый взгляд. Вот хотя бы на интервале $\left ( \sqrt{c}+\sqrt{d},\sqrt{m} \right )$. Близость (соседство) подобных иррациональностей на числовой оси выражается уравнением $\sqrt{a}+\sqrt{b}+\sqrt{c}+\sqrt{d}\approx 0$, или в целых числах $64abcd\approx \left ( 2(a+b)(c+d)-(a-b)^2-(c-d)^2 \right )^2,$ из чего видно, что для "очень тесных" пар произведение $64abcd$ близко к целому квадрату. Последовательность таких квадратов также вызывает интерес. И главное. В уравнении $\sqrt{m} \approx \sqrt{x}+\sqrt{y}\ \ (1)$ из начала темы все три параметра целые. Если допустить рациональное $y$, задача превращается в упражнение на разложение в цепную дробь. Но если переместить дробное значение в левую часть, всё оказывается интересней. Запишем:

$$\alpha \approx \sqrt{x}+\sqrt{y}\ \ \ (4),$$

где $\alpha$ — рациональный аргумент, $0<x<y$ — целые. Прежде напомню кое-что из теории непрерывных дробей. Период разложения квадратного корня из рационального числа $>1$ есть палиндром с нулем: $u_0,u_1,...,u_n,...,u_1,u_0,0.$ И обратно. Нечетные периоды для данной задачи неактуальны. $u_0$ — целая часть. Число $0$ в практике не используется, поэтому в стандартной записи возникает знак $2u_0$, знаменуя конец/начало периодов. Нас же в основном интересует внутренний палиндром $u_1,...,u_n,...,u_1,$ который есть приближение обратной величины дробной части: $\approx a_0+\dfrac{1}{u_1,...,u_n,...,u_1}.$ Все сказанное справедливо и для целого радикала, но оказывается, вовсе не любой палиндром может быть дробной частью целого радикала. Поясню. Две последние подходящие дроби палиндрома имеют вид $u_1,...,u_n,...,u_1=...\dfrac{B}{C},\dfrac{A}{B}.$ Если знаменатели $B,C$ нечетные, то не может. В противном случае можем вычислить варианты целой части $u_0$, которые образуют арифметическую прогрессию: $u_0 \equiv -BC/2 \pmod A$ в случае нечетного $A$, и $u_0 \equiv -BC/2 \pmod {A/2}$ в случае четного $A.$ Таким образом возможно "восстановить" целый радикал по его дробной части. Подробнее об этом было здесь. Теперь к задаче. Возводя почленно в квадрат обе части $(4),$ получаем $\alpha^2 \approx x+y+\sqrt{4xy}.$ Обозначим $x+y=s,x-y=v.$ Новое уравнение выглядит так:

$$\alpha^2 \approx s+\sqrt{s^2-v^2}\ \ \ (5).$$

Дробная часть радикала — палиндром, значит чем лучше приближение, тем "яснее" в дробной части разложения $\alpha^2$ должен читаться палиндром. И тем ближе к $\alpha$ находится иррациональность вида $\sqrt{a}+\sqrt{b}.$ Тут, однако, самая плохо формализуемая часть задачи — надо помнить хотя бы о приведенной и не приведённой записях: $u_1,u_2,...,u_n=u_1,u_2,...,u_n-1,1.$ Возникающие ограничения оставим на потом. Разложение $\alpha^2$ — конечная дробь, в которой, допустим, удалось разглядеть палиндром от второго знака. Тогда в разложении $\sqrt{s^2-v^2}=u_0,u_1,...,u_n,...,u_1$ нам известны все знаки кроме $u_0$, а его (их) можно вычислить выше указанным способом. Из $s+u_0=\left \lfloor \alpha^2 \right \rfloor$ следует $s=\left \lfloor \alpha^2 \right \rfloor-u_0.$ Ну, а имея на руках $s$, получаем из $(5)$ $v=\alpha\sqrt{2s-\alpha^2}$ и, помня что $x,y=\dfrac{s \mp v}{2}$, имеем окончательно

$$x,y=\dfrac{s \mp \alpha\sqrt{2s-\alpha^2}}{2}\ \ \ (6).$$

Примеры.
$1$) Решим приближение $\dfrac{161}{29} \approx \sqrt{x}+\sqrt{y}.$
Разложим $\dfrac{161^2}{29^2}=30,1,4,1,1,...$ В дробной части видим палиндром из трех знаков $1,4,1=\dfrac{1}{1},\dfrac{5}{4},\dfrac{6}{5}.$ Из двух последних знаменателей один четный, значит палиндром может выражать (приближать) дробную часть целого радикала. Вычислим возможные целые части: $-4 \cdot 5/2 \pmod {6/2} \equiv -10 \pmod {3} = 2,5,8,11,14.$ Тут нужно заметить, что $s > \sqrt{s^2-v^2} >u_0,$ поэтому $s>\left \lfloor \alpha^2 \right \rfloor/2>u_0.$ Все варианты $u_0<30/2$ у нас перечислены, и начинать проверку лучше с наибольшего. $s=30-14=16.$ Подставляя $s=16,\alpha=161/29$ в $(6),$ получаем x $\approx 5,y \approx 11$ и разложение $\sqrt{5}+\sqrt{11} \approx 5,1,1,4,4,...=5,1,1,4,3,1,...\approx \alpha$ с точностью до не приведенного. Остальное можно не проверять.
$2$) Решим приближение $\dfrac{1329}{113} \approx \sqrt{x}+\sqrt{y}.$
Разложим $\dfrac{1329^2}{113^2}=138,3,9,1,411.$ Палиндромы $3,9,1,411,1,9,3$ и $3,9,1,410,1,9,3$ (от не приведенного) возвращают $u_0>\alpha$, что ведет к отрицательному $s.$ Палиндром $3,9,1,9,3$ возвращает два нечетных знаменателя в последних подходящих. Остается "подогнать" $3,9,3.$ Подобное творчество в математике хуже перебора, согласен. Но разложим-таки $3,9,3=\dfrac{3}{1},\dfrac{28}{9},\dfrac{87}{28}.\ \ \ -9 \cdot 28/2 \pmod {87}=48.$ Подставляя $s=138-48=90,\alpha=1329/113$ в $(6),$ имеем $x,y=7,83$ — неплохое приближение, в принципе, но не лучшее.

Ситуация складывается следующая. Любой нечетный палиндром имеет "вершинку" — подпоследовательность $u_{n-1},u_n,u_{n-1}$, которая сама по себе суть мини-палиндром из трех знаков. Будем раскладывать $\sqrt{a}+\sqrt{b}$, выписывая по ходу дела разложения квадратов подх. дробей. По мере увеличения точности они всё более будут совпадать за исключением $1$-го знака с разложением $\sqrt{4ab}$ (которая есть палиндром) и в какой-то момент $=N(a,b)$ достигнут "вершинки" $u_{n-1},u_n,u_{n-1}.$ Такая дробь уже различима для предложенного алгоритма, как и все последующие. Будем называть их "вычислимыми" относительно данного алгоритма или, попросту, различимыми (кому как удобно). Сразу замечу, что показатель $N()$ выражает свойство пары целых положительных чисел (не обязательно вз. простых), различимость же — свойство самой рациональной точки. Мало ли в какие разложения она еще может входить (единственность не доказана). Зато, не встретив ни одного мини-палиндрома в разложении $\alpha^2$, можем точно сказать, что сия $\alpha$ неразличима. Дробь из $2$-го примера тоже неразличима, хотя $\dfrac{1329^2}{113^2}=138,3,9,1,411=138,3,9,\overline{1,410,1},$ что нуждается в проверке. Дробь из первого примера различима. Вычислим $N(x,y).$
$\sqrt{5}+\sqrt{11}=5,1,1,4,4,11,...=\dfrac{5}{1},\dfrac{6}{1},\dfrac{11}{2},\dfrac{50}{9},\dfrac{211}{38},...\ \ \ \sqrt{4 \cdot 5 \cdot 11}= 14,\overline{1,4,1},...$
Первая дробь — всегда целое, а нас интересуют дробные части: $\dfrac{6^2}{1^2}=36;\dfrac{11^2}{2^2}=30,4;\dfrac{50^2}{9^2}=30,1,6,...;\dfrac{211^2}{38^2}=30,1,4,1,...$ Можно бы записать $N(5,11)=4,$ но тут возникает неточность. Ведь в первом примере фигурировала иная дробь $161/29,$ из который был получен нужный палиндром. Ранняя (с меньшим знаменателем). Она возникает из неприведенной записи $\sqrt{5}+\sqrt{11}=5,1,1,4,3,1...,$ и как-то надо это помечать. Например апострофом: $N(5,11)=4',$ Не знаю, на сколько может быть востребован этот параметр, но пусть будет. Что еще? Да, по поводу "лучшести". Я исходил из того, что если разложение $\alpha$ входит в разложение $\sqrt{a}+\sqrt{b},$ то она (иррациональность) лучшая, но таких может быть не одна. Не знаю. Пока не думал. Качество аппроксимации, кстати, хорошо заметно уже на выходе при подстановке данных в формулу $(6).$

Да, и еще по поводу различимости. Некоторые дроби вообще не могут входить в разложение рассматриваемых иррациональностей. Например $\alpha<2.$ Считаем их также неразличимыми, но совсем списывать со счетов последние не стоит. Получено же во $2$-м примере некое приближение. Понятно, что среди "маленьких" дробей (с малыми элементами) будут преобладать неразличимые. Но! Нужно понимать, что из разложения $\sqrt{a}+\sqrt{b}$ получаем лишь конечное число неразличимых и бесконечно много различимых — все подходящие с номером $>N(a,b)$, а с некоторого момента, думаю, и все промежуточные. Каково их соотношение на множестве $\mathbb{Q}$ — вот вопрос достойный философа ) Возвращаясь к первоначальной задаче, положим, имеется некоторое приближение $\sqrt{a}+\sqrt{b}\approx \sqrt{m}.$ Что нам мешает вычислить срединную точку $(\sqrt{a}+\sqrt{b}+\sqrt{m})/2$ и получить дробь нужной точности? Хорошо бы представить ее алгебраическим числом (видимо $8$-й степени), а раскладывать алгебраические числа мы умеем. Займусь этим на досуге. Не думаю, что будет легко, точный инструмент требует точных данных, среднее арифметическое тут слишком грубо. Но об этом после. Хорошо, если бы удалось уйти от квадратичных вычетов.

[Andrey A]

Andrey A в сообщении #1590015 писал(а):

... представить ее алгебраическим числом (видимо $8$-й степени)

Так и есть, но соотв. уравнение настолько громоздко и непрактично, что и приводить не стану. Тем более, что среднее арифметическое взято с потолка, есть более изящные способы локализовать точку на интервале $\left ( \sqrt{a}+\sqrt{b},\sqrt{m} \right ).$ Ограничим интервал дробями: $\left ( \dfrac{a-b}{\sqrt{a}-\sqrt{b}},\dfrac{m}{ \sqrt{m}} \right ),$ а лучше так: $\left ( \dfrac{a-b}{\sqrt{a}-\sqrt{b}},\dfrac{zm}{ z\sqrt{m}} \right ).$ От величины $z$ границы интервала не зависят (считаем их положительными числами), но медианта $\dfrac{a-b+zm}{\sqrt{a}-\sqrt{b}+z\sqrt{m}}\ (7)$ может выражать любую точку $\beta$ на заданном интервале, даже искомую $\beta=\sqrt{x}+\sqrt{y}$. Продолжение логики цепных дробей на нерациональные дроби, $z$ — аналог остатка дроби. Решая уравнение $\dfrac{a-b+zm}{\sqrt{a}-\sqrt{b}+z\sqrt{m}}=\beta$ относительно $z$, получаем $z=\dfrac{ \sqrt{a}-\sqrt{b}}{\sqrt{m}} \cdot \dfrac{\beta - \sqrt{a}-\sqrt{b}}{\sqrt{m}-\beta}.$ Обозначим последний множитель буквой $k=\dfrac{\beta - \sqrt{a}-\sqrt{b}}{\sqrt{m}-\beta}>0.$ Искомая точка делит заданный интервал на два отрезка. Отношение этих отрезков $=k,\ z=k \dfrac{ \sqrt{a}-\sqrt{b}}{\sqrt{m}}.$ Подставляя это в $(7),$ получаем $\beta=\dfrac{a-b+k\sqrt{m}(\sqrt{a}-\sqrt{b})}{\sqrt{a}-\sqrt{b}+k(\sqrt{a}-\sqrt{b}),}$ что можно еще сократить на $\sqrt{a}-\sqrt{b}$. В итоге имеем:

$$\sqrt{x}+\sqrt{y}=\dfrac{\sqrt{a}+\sqrt{b}+k\sqrt{m}}{1+k}\ \ (7)$$

и обратная связь:

$$k=\dfrac{\sqrt{x}+\sqrt{y}-\sqrt{a}-\sqrt{b}}{\sqrt{m}-\sqrt{x}-\sqrt{y}}\ \ (8)$$

Ситуация ожидаемая: чем хуже приближение $\sqrt{a}+\sqrt{b} \approx \sqrt{m}$, тем больше ирр-ей нужного вида на заданном интервале, и с хорошей вероятностью попадаем в "зону притяжения" одной из них произвольным $k$
( $k=1$, кстати, дает среднее арифметическое). Если же искомая единственная (лучшая), то $k$ придется задать с приличной точностью. Ну, а если ее нет вообще (тест на простоту), то уж и не знаю... самый трудноустановимый факт.

На грани целого часто приходится работать с мини-палиндромом вида $1,t,1.$ Значения $u_0$ для него можно выписать в общем виде:
Для нечетного $t\ \ u_0=t+1 \pmod {t+2}.$
Для четного $t\ \ u_0=t/2 \pmod {t/2+1}.$