junaЭто верно, конечно, но имелось в виду другое. Нам известно, что в решениях

произведение

есть число вида

Если

то

— треугольное число

. То же и

Рассмотрим случаи, когда треугольное число

имеет ровно два простых делителя (для этого нам нужны простые Софи Жермен и похожая последовательность
oeis.org/A005382). Все приближения вида

для них имеют иксом двойку, но в некоторый момент они перестают быть решением, это как раз первое квазипростое, указанное Вами. Следующее решение (

) не является квазипростым, если не ошибся:

Если они так и дальше идут вперемешку, можно сделать вывод о бесконечном числе вхождений двойки в решения вида

Но ключевое отношение

увеличивается, и мне это кажется нелогичным. Вот проверил дальнейшие
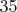
треугольников до

, все они уже оказались квазипростыми. Если же предположение о конечном числе вхождений двойки в

верно, то по простым

и подавно. Другие числа ничем не хуже двойки, и тогда можно говорить о верхней границе отношения

как функции от

. Может, она даже к чему-то сходится — понятие "не может быть слишком большим" мало к чему обязывает. Как-то так.