Пользуясь определением нелинейной функции от оператора, показать, что
![$[\hat{x},F(\hat{p})] = i\hbar\frac{dF(\hat{p})}{d\hat{p}}$ $[\hat{x},F(\hat{p})] = i\hbar\frac{dF(\hat{p})}{d\hat{p}}$](https://dxdy-02.korotkov.co.uk/f/9/9/5/995eda0523c5a2ca55f6bf8dd9cda3b682.png)
Я решил рассмотреть вид оператора
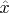
в импульсном представлении, когда волновая функция зависит от проекций импульса:
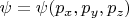
,
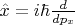
Т.к. у нас
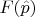
- функция зависящая от оператора импульса, то и сам оператор
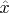
я решил будет зависеть от оператора импульса и по аналогии с
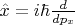
получится, что
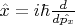
Тогда, по аналогии с коммутатором 2-х операторов
![$[\hat{x},\hat{{p}_{x}}] = i\hbar$ $[\hat{x},\hat{{p}_{x}}] = i\hbar$](https://dxdy-02.korotkov.co.uk/f/9/4/0/9401fc418efbb42d908bae7b3fdf531982.png)
(который получается из следующих соображений:
![$[\hat{x},\hat{{p}_{x}}]\psi= (\hat{x}\hat{{p}_{x}} - \hat{{p}_{x}}\hat{x})\psi = x(-i\hbar\frac{d}{dx})\psi - (-i\hbar\frac{d}{dx})x\psi = -i\hbar x(\psi)' + i\hbar\psi + i\hbar x(\psi)' = i\hbar\psi \to [\hat{x},\hat{{p}_{x}}] = i\hbar$ $[\hat{x},\hat{{p}_{x}}]\psi= (\hat{x}\hat{{p}_{x}} - \hat{{p}_{x}}\hat{x})\psi = x(-i\hbar\frac{d}{dx})\psi - (-i\hbar\frac{d}{dx})x\psi = -i\hbar x(\psi)' + i\hbar\psi + i\hbar x(\psi)' = i\hbar\psi \to [\hat{x},\hat{{p}_{x}}] = i\hbar$](https://dxdy-04.korotkov.co.uk/f/3/7/7/37751cd706099d6faa2cc219feeb079282.png)
)
Я могу получить:
![$[\hat{x},F(\hat{p})]\psi = (\hat{x}F(\hat{p}) - F(\hat{p})\hat{x})\psi = i\hbar\frac{dF(\hat{p})}{d\hat{{p}_{x}}}\psi + i\hbar\frac{d\psi}{d\hat{{p}_{x}}}F(\hat{p}) - F(\hat{p})i\hbar\frac{d\psi}{d\hat{{p}_{x}}} = $ $[\hat{x},F(\hat{p})]\psi = (\hat{x}F(\hat{p}) - F(\hat{p})\hat{x})\psi = i\hbar\frac{dF(\hat{p})}{d\hat{{p}_{x}}}\psi + i\hbar\frac{d\psi}{d\hat{{p}_{x}}}F(\hat{p}) - F(\hat{p})i\hbar\frac{d\psi}{d\hat{{p}_{x}}} = $](https://dxdy-03.korotkov.co.uk/f/a/0/a/a0afc7facb9981531b962ad43315030682.png)
![$ = i\hbar\frac{dF(\hat{p})}{d\hat{{p}_{x}}}\psi \to [\hat{x},F(\hat{p})] = i\hbar\frac{dF(\hat{p})}{d\hat{{p}_{x}}} $ $ = i\hbar\frac{dF(\hat{p})}{d\hat{{p}_{x}}}\psi \to [\hat{x},F(\hat{p})] = i\hbar\frac{dF(\hat{p})}{d\hat{{p}_{x}}} $](https://dxdy-01.korotkov.co.uk/f/8/d/5/8d5b24b9ebcd03ca2f1956907037b8ba82.png)
Правильно ли мое доказательство?
Верно ли полагать, что оператор
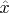
можно представить не через проекцию импульса, а через оператор импульса
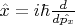
?
И смущает еще то что, по итогу у меня получилось
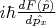
, а не
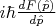
или это не критично?
Или же мой ход доказательства неверный и доказывать надо отталкиваясь от чего-то другого?