Сел. Прочитал. Вычитал следующее:
Всё множество ПТ делится на разряды, у каждого своя закономерность чередования троек
Это в каких же книгах вы такое вычитали?
Напоминаю, я приводил формулы только для первого разряда ПТ; для тех, у которых

Раз напоминаете, то можете дать ссылку, где про это было написано? (там же наверное и обозначения расшифрованы?)
Я всего лишь предложил простой способ генерации ПТ (без их лихорадочного поиска в Инете) для некоторого класса (или разряда) ПТ
Это, конечно, хорошо, но есть известный способ генерации всех (примитивных) троек:

,

,

(здесь

нечетное,

четное, гарантий на то, что
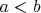
, нет).
И например ваше
m = a /2


получается подстановкой сюда

.
-- 29.12.2022, 11:20 --Andrey A, я нашел эту статью. Там всего две страницы, которые я внимательно прочитал только чтобы в самом конце увидеть
Цитата:
при

в числителях имеем разность двух нечетных чисел, т.е. четные числа, в знаменателях всегда нечетные числа, а это означает, что частное от деления не может быть целым числом
Но признаюсь, не зря потратил время, таких рассуждений я даже у ChatGPT не видел.
По сути же там пытаются показать что из

(где

и

вроде бы связаны с гипотезой Била, но я не очень понял, как) для нечетных

и

следует

.