1.
Посмотрите
тут, какие ещё изобретены способы построить двухэтажный дом из песка.
Спасибо! Там сказано, что свойство "

-- первый элемент пары" формулируется как

, так что в выражении

первый элемент пары это

.
1. Возьмите два множества,

и

. Считая, что все элементы
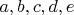
различны, запишите, прямо по определению, какую-нибудь функцию

как множество, используя определение пары по Куратовскому.
Запишу две, инъективную:

и неинъективную:

.
2. Запишите, опять же по определению, какую-нибудь функцию

.
Запишу две (их всего две):

,

. Не знаю, правильно ли записал.
Детская задача писал(а):
У меня две монеты на общую сумму 15 копеек. Одна из них не пятак. Что это за монеты?
По 10 и по 5 копеек.
2.
Значит определение
Цитата:
Функция в математике — соответствие между элементами двух множеств — правило, по которому каждому элементу первого множества, называемого областью определения, соответствует один и только один элемент второго множества, называемого областью прибытия.
неполное, надо пользоваться определением "

- подмножество

, такое

" (которое помещено у Верещагина-Шеня).
Полное, просто неформальное. У нас действительно есть правило, по которому мы каждому элементу пустого множества что-то сопоставляем. Просто раз элементов нет, то и сопоставление пустое.
Здесь Вы признаете существование несуществующих объектов: несуществующим элементам пустого множества Вы что-то сопоставляете.
("Существование несуществующих объектов" -- это само в себе противоречивое выражение, но если мы имеем дело с несуществующими объектами: сопоставляем им что-то, -- значит, мы в каком-то смысле признаем, что они существуют.)
Если же не признавать существования несуществующих объектов, то, мне кажется, определение из Википедии все-таки неполное, по нему функция это соответствие между существующими элементами двух множеств, значит, если нет элементов, нет и соответствия (а не то, что соответствие есть, но оно пустое), то есть нет функции.
Если не признавать существование несуществующих объектов, то определение из Википедии неполное, потому что в нем ничего не говорится об отображении между множествами

и

в случае, когда одно из них пусто или они оба пусты.
А если признавать, то, как вы сами сказали,
Такая система должна очень сильно отличаться от всего используемого в математике,
так что вряд ли авторы определения из Википедии основывались на ней.
Определение из Верещагина-Шеня (
https://www.mccme.ru/free-books/shen/sh ... art1-2.pdf стр. 32)
Цитата:
Отношение

называется функцией из

в

, если оно не содержит пар с одинаковым первым членом и разными вторыми.
хитрее, под него попадает и пустое множество: оно не содержит ни одной пары и, значит, не содержит пар с одинаковым первым членом и разными вторыми.
Для справки:
Цитата:
Любое подмножество

множества

называется отношением между множествами

и

(в том числе и пустое подмножество).