Выходит, в первом случае обратная задача решается на пятерку, а тут затык... это как минимум странно. Просто она сложная.
Но не безнадежная. Напомню:
Обозначим

и приравняем остатки дробей разложений

и


После тотального взаимоуничтожения переменных получаем хорошо знакомое

при бесконечно малом

Дальше такая высшая математика пошла, что без стакана было не обойтись. Я-то почти не пью, а тут пришлось, и кажется впрок. Всех с Новым Годом! Наутро подумалось примерно так: выражение

суть убывающая погрешность разложения

. Равенство

позволяет избавиться от переменной

. Подставляя в первое

и приравнивая его к нулю, получаем линейное уравнение относительно

, но

следует брать не бесконечно малым, понятно, а реально отвечающим условию задачи. И вот оказалось, оно отлично работает:

Рискнул поставить точное равенство, хотя не уверен что последовательность сходится именно к целой точке, но к очень близкой. Впрочем, пока проверял только случаи

Выражение верно для последовательности подходящих дробей

разложения

, а зная

легко получаем искомые

с помощью равенств

Так что обратная задача решена. Но! Этих "но" тут с лихвой, и главный вопрос оказался вовсе не пустяковым: сколько верных дробей содержит разложение

действительно ли их "станет хватать" при достаточно больших модулях и что делать, если это не так. Для

их всего

(даже меньше чем для

), а нужно

Сильно против работает присутствие больших знаков дроби (в разложении

их два:

). Короче, нужен анализ статистики, тут вся моя надежда на сообщество. Заранее признателен! Есть и хорошие новости:
— Для положительного

достаточно исследовать только нечетные дроби

, остальные случаи пока не разбирал, но всё к тому что четные понадобятся для

(верхние приближения), а
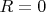
— пожалуйста и те и другие. Члены последовательности

ложатся на некоторую плавную кривую, которая в искомой целой точке

почти вырождается в прямую параллельную оси

(абсцисс). Если бы удалось экстраполировать ее по нескольким начальным значениям — это было бы отличное, действительно аналитическое решение.
И пока хватит. Мало ли, может не всем попалась такая хорошая водка ) "Зона совпадения знаков" всё-таки должна расти, но похоже, и необходимое количество знаков не стоит на месте. Самый трудный вопрос.