I noticed also that it can save some time (including in many cases an ispseudoprime check) if you look at
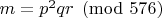
at the very start, and continue testing only if
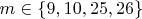
. That is enough to verify that the

of
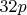
is not divisible by 2 or 3, and that
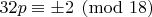
. (I'm fairly sure I have the right values for

, after stepping through a handful of cases.)
I question these 4 values of yours. At least 9 and 10. Let's do the math:
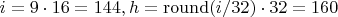
,
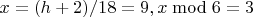
- not 1 or 5!
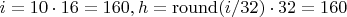
,
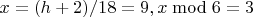
- not 1 or 5!
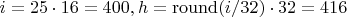
,
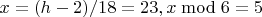
- ok.
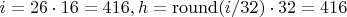
,
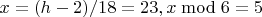
- ok.
The case
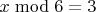
is excluded because 3 is already in 18 and the remaining unknown prime cannot be a 3 (then it would increase the power of 3 here and the divisors would definitely not be 12) and cannot have a remainder 3 modulo 6 (there is only one prime, 3 itself, which is already excluded).
No decisions are missed, but the work is half as slow as possible.
But: we don't need
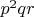
if they get further than 7 from
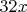
, i.e. 400-408 is unnecessary, as is 424-431.
This leaves only 409-423 modulo 576 acceptable:
Код:
? for(i=0,576-1, n=round(i/32); h=32*n; x=round(h/18); if(abs(h-i)<8 && (n%6==1 || n%6==5) && (x%6==1 || x%6==5), print1(i,", ")))
409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419, 420, 421, 422, 423,
Of all these, can actually be found in
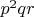
only such::
Код:
? m=vector(576); forstep(p=1,#m,2, if(p%6==3, next); forstep(qr=1,#m,2, if(qr%6==3, next); x=(p^2*qr)%576; m[x+1]=x)); print(select(x->(x>408 && x<424), Set(m)))
[409, 413, 415, 419, 421]
-- 25.11.2022, 14:34 --The calculation time of the pattern with the same LCM will increase by 12 times. This is with a naive linear approximation. Rather, the growth will be
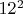
or so.
Для них можно ровно так же взять и ограничить простые, хоть до тех же 5e8. Это будет сильно дольше, но ведь всего один раз посчитать. И тогда интервал квадратичных переборов будет идентичен. А вся разница будет только из-за линейных переборов, которые должны давать примерно линейное время, т.е. всё же примерно в 12 раз, не 144.