fred1996, спасибо за интересную задачу. Расскажу в двух словах, как решал. Сначала не предполагал

(надеялся решить точно). Обозначим костяшки

и

.
1) Рассмотрим этап, когда костяшки уже в контакте. Пусть

и

— углы отклонения

и

от вертикали. Тогда геометрическая связь

.
Продифференцируем её по времени:

Сразу после столкновения

вертикальна,

, откуда

. Значит, сразу после столкновения угловые скорости костяшек равны.
2) При ударе каждая костяшка действует на другую в течение малого времени с большой силой, направленной горизонтально (нет трения).
Плечо силы

относительно оси вращения

равно плечу силы

относительно оси вращения

.
Поэтому момент импульса, полученный при ударе

, равен минус моменту импульса, полученному

(притом, что момент импульса каждой костяшки вычисляется относительно "своей" оси вращения).
Отсюда с учётом 1) следует, что угловая скорость

при ударе уменьшилась вдвое. Следовательно, при ударе ровно половина кинетической энергии рассеялась (четверть осталась у

и четверть перешла к

).
3) Рассмотрим 3 положения костяшек:
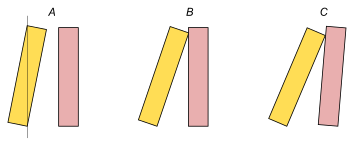

:

в максимуме потенциальной энергии и только-только начинает падать.

в исходном положении.

: костяшки только что соприкоснулись.

: костяшки в контакте достигли максимума суммарной потенциальной энергии. Если они через него перевалят, дальше точно будут падать.
Замечание: если  достаточно велико, положения
достаточно велико, положения  может не существовать (оно сливается с
может не существовать (оно сливается с  ).
).Из 2) получаем, что костяшки преодолеют

и упадут вместе, если

. Значению

, когда его "только-только" хватает для падения обеих костяшек, соответствует знак равенства.
Остаётся найти

.
4) Приближение: предположим, что

и угловые скорости костяшек остаются равными (но не постоянными) вcюду от

до

. Тогда будет постоянным угол между вектором из оси вращения

в её центр масс и вектором из оси вращения

в её центр масс. И легко найти максимум

суммарной потенциальной энергии во время движения костяшек в контакте, даже не находя положения

, при котором этот максимум достигается.
Дальше довольно просто.