Как видно в последних двух приведенных строчках, в позицию с

подставляются квадраты больших простых. И эти большие простые будут ограничены

.
Но мы же в предрасчете не проверяли для

...
Проверяли:

в цикле идёт от

, а

от

(но не меньше чем

) до

для каждого

, так что все варианты

были проверены при

. И у меня принято что

, я об этом прямо сказал, возможно из-за этого у Вас некоторая путаница.
завязано на том, что в паттерне обязательно есть "пустое" место, куда буде расставляться
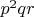
, а

Нет, это завязано на том что в любой непустой позиции есть простое не меньше

, а после подстановки

останется неизвестное простое не меньше

.
В пустую позицию подставляться будет

, а

там может быть не менее чем

(все меньшие простые уже расставлены).
Запустил расчет ранее посчитанного паттерна b2155 теперь с ключом -p1^1000000001
Ускорение в разы наблюдается, но не в 40-50 раз. На первых записях в лог ускорение было в 7-8 раз. Сейчас колеблется в районе 3-5 раз.
Во первых там вроде бы двоеточие должно быть. Во вторых не от 1 (впрочем это неважно). В третьих я запускал с ключом -g3, он оказался быстрее -g9 и -g16. В четвёртых возможно дальше ускорение будет выше, я же сравнивал только конечный результат. В пятых я не обещал ускорения 40-50 раз на всех паттернах, на паттернах с одним перебором оно будет меньше 6х (ускорится только конец первого перебора и всё). В шестых имеет смысл поиграться с -g, теперь ведь второй-третий перебор можно запускать чаще прежнего, они же быстрее выполняются (т.е. можно посмотреть на первые 10-20 минут в логе и сравнить сколько времени занял линейный поиск и сколько квадратичный и не стоит ли уменьшить/увеличить -g).
-- 19.11.2022, 23:24 --В пятых я не обещал ускорения 40-50 раз на всех паттернах, на паттернах с одним перебором оно будет меньше 6х (ускорится только конец первого перебора и всё).
Но возможно будет выгодно запустить второй перебор (указанием соответствующего -g) и тогда выигрыш может станет и больше. А может и не стать, если линейный перебор для каждого простого и так был быстрее квадратичного с ограничением

.
Да, про то что выигрыш будет 45 раз на
любых паттернах я погорячился. Где-то меньше, где-то больше. Я же не проверял их все.
-- 19.11.2022, 23:29 --EUgeneUSВ начале много линейных переборов, а они не ускоряются. Вот когда линейных переборов станет меньше, останутся лишь квадратичные, вот они то и ускорятся. И так на каждом уровне перебора.
-- 19.11.2022, 23:34 --Вообще этот ключик -g очень мутный и непонятно как его выбирать кроме как опытным путём.

Когда я буду делать такой универсальный перебор, то склоняюсь всё же к автоматическому выбору на лету, прямо по реальному счёту или тестовому измерению.
-- 19.11.2022, 23:43 --Ну и да,

я проверил, можно пользоваться ключом -p1e9.
-- 19.11.2022, 23:49 --А может я вообще ошибся в своих тестах и ускорение меньше.
