Если совсем лениво, то можно вот так:

Нужно, чтобы столбцы матрицы
A были линейно независимы (иначе обратной матрицы не будет существовать). Тогда решение будет удовлетворять условию наименьших квадратов:

Почему вы зовёте такой подход ленивым? Разве в большинстве случаев он не единственный?
Не, не единственный, ленивый, и очень не популярный в вычислительной математике. Смотрите, пусть

имеет обусловленность близкую к обратному значению машинной арифметики. Теоретически - матрица

все еще не вырожденная, решение может быть, но вот если построить

, то ее обусловленность будет уще больше обратного машинного эпсилона, и Холецкий, даже с полным пивотированием гарантированно упадет. Да в любом случае, очень не правильно плохо обусловленную задачу приводить к такой, у которой обусловленность в квадрат выше, поэтому я назвал этот метод ленивым.
Правильно делать через
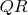
. Конечно можно через SVD, но метод через SVD численно требует больше арифметических операций, поэтому если делать правильно, лучше через QR.
Алсо, в Матлабе, я смотрю, нет необходимости всё это дело вручную прописывать:
mldivide вполне справляется в лоб:
Надо взять на вооружение и не плодить сущности без необходимости.
А вот ХЗ как матлаб это реализовал, поэтому я бы не советовал бы в случаях с плохой обусловленностью исходной матрицы :)
Алсо, QR-алгоритм применим же только к квадратной обратимой матрица A, разве нет?
Есть два QR - первый для построения ортогональной

и верхней треугольной

, второй - как один из шагов для итерационного поиска собственных значений.
Так как у них теория одинакова, их часто одинаково называют, некоторые правда чтобы разделить называют так, что типа первый - это QR-разложение, второй QR-алгоритм, я правда на американский манер не разделяю и все называю QR, правда я же уточнил, что это - ортогонализация, то есть именно первый имел ввиду.
Холецкий для

Спасибо за наводку, не знал! Это разложение ещё позволяет посмотреть на величину диагональных элементов и сообразить, когда и как матрица
H близка к сингулярной.
[/quote]
пока вы делаете Холецкого без пивотинга диагонального элемента, вы почти всегда будете видеть в качестве обусловленности погоду на Марсе, то есть оценка по диагонали Холецкого обычно сильно завышена.
Простой пример

И даже полное пивотирование тоже часто дает завышенную оценку, смотрим на матрицу с единичной обусловленностью:




