Разложение Фурье, нахождение гармоник, прогноз

[B@R5uk]

ilghiz в сообщении #1565638 писал(а):

если частота может медленно изменяться во времени, то Фурье дает очень размазанный пик

Ну, при некоторой ловкости рук Фурье даже меняющуюся частоту переваривает. Вот, например, реальный образец голоса и выделение первой гармоники из него:

Mi.wav (48 кГц, 56 КБ)





view_signal.m

Используется синтаксис Matlab M

clc
clearvars
format compact

blocksize = 512;

[wdata, fs, nbits] = wavread ('Mi.wav');
dsize = size (wdata, 1);

bnum = floor (dsize / blocksize) - 4;
env = 0.5 * (1 - cos (2 * pi * ((1 : 4 * blocksize)' - 0.5) / (4 * blocksize)));

spec = zeros (4 * blocksize, bnum);
for k = 1 : bnum
    spec (:, k) = fft (env .* wdata ((k - 1) * blocksize + (1 : 4 * blocksize)));
end

spec_amp = abs (spec (1 : 2 * blocksize, :));
spec_sel = spec_amp > 2.5;
spec_sel (1 : 3, :) = 0;
spec_sel (11 : end, :) = 0;
spec_sel (9 : end, 13 : end) = 0;
if 1
    imdata = log10 (spec_amp) * 15 + 30;
else
    imdata = log10 (spec_amp) * 0.3 + 0.4;
    imdata = cat (3, spec_sel * 0.8, imdata, imdata);
    imdata = max (0, imdata);
    imdata = min (1, imdata);
end

subplot (4, 1, 1:3)
image (imdata (1 : 160, :, :))
axis xy

subplot (4, 1, 4)
plot (max (spec_amp))
xlim ([0.5, bnum + 0.5])
 

split_harms.m

Используется синтаксис Matlab M

clc
clearvars
format compact

blocksize = 512;

[wdata, fs, nbits] = wavread ('Mi.wav');
dsize = size (wdata, 1);

bnum = floor (dsize / blocksize) - 4;
env = 0.5 * (1 - cos (2 * pi * ((1 : 4 * blocksize)' - 0.5) / (4 * blocksize)));

spec = zeros (4 * blocksize, bnum);
for k = 1 : bnum
    spec (:, k) = fft (env .* wdata ((k - 1) * blocksize + (1 : 4 * blocksize)));
end

spec_amp = abs (spec (1 : 2 * blocksize, :));
spec_sel = spec_amp > 2.5;
spec_sel (1 : 3, :) = 0;
spec_sel (11 : end, :) = 0;
spec_sel (9 : end, 13 : end) = 0;

spec_harm = spec .* [spec_sel; zeros(1, bnum); flipud(spec_sel (2 : end, :))];
hdata = zeros (dsize, 1);
for k = 1 : bnum
    addr = (k - 1) * blocksize + (1 : 4 * blocksize);
    hdata (addr) = hdata (addr) + env .* real (ifft (spec_harm (:, k)));
end
hdata = hdata / 1.5;

cycle = round (2 * pi / sqrt (-sum ([0; diff(hdata, 2); 0] .* hdata) / sum (hdata .^2)));
%vect_cos = cos (2 * pi * (1 : dsize)' / cycle);
%vect_sin = sin (2 * pi * (1 : dsize)' / cycle);

hdata_hlb = hilbert (hdata);
hdata_amp = abs (hdata_hlb);
hdata_phs = unwrap (angle (hdata_hlb));
hdata_frq = diff ([0; hdata_phs]) * fs / (2 * pi);
args = (1 : dsize)';
args_sub = args (hdata_amp > 0.002 & args > 5100);
tt = args / fs;
tt_sub = args_sub / fs;

subplot (211)
plot (tt, wdata, 'g')
hold on
plot (tt, hdata_amp, 'r', 'LineWidth', 2)
plot (tt, hdata, 'k')
hold off
xlim ([0, tt(end)])
ylim ([-0.4, 0.6])
grid on
title ('Voice sample and 1st harmonic graphs')
legend ('signal', '1st h. amplitude', '1st harmonic')
ylabel ('Amplitide, r.u.')

subplot (212)
plot (tt_sub, hdata_frq (args_sub), 'LineWidth', 2)
xlim ([0, tt(end)])
grid on
title ('Harmonic frequency graph')
legend ('1st harmonic')
xlabel ('Time, sec')
ylabel ('Frequency, Hz')
 

[Schrodinger's cat]

svv понятно.
Но в программе это я так понимаю не нужно, у нас уже есть вектор коэффициентов $a$, относительно которого можно построить полином. Этот вектор отправляю в polyroots mathcad'a получаю новый вектор, так понимаю нашел z.
Но что то пока ничего не получается, ничего подобного ни на изначально заданную частоту, ни на коэффициенты затухания... Что то я делаю не так...
А вот SVD этой Теплицевой матрицы дает 2 положительных сингулярных числа.

[ilghiz]

Schrodinger's cat в сообщении #1565737 писал(а):

А вот SVD этой Теплицевой матрицы дает 2 положительных сингулярных числа.

Вот позвольте предложить как вам проверить этот метод.

1. пусть у нас есть вектор из $N$ комплексных отсчетов и он содержит 2 комплексные экспоненты плюс какой-то шум.
2. Строим по нему Теплицеву матрицу размера $(N-2) \times 3$ вида $a_{ij} = f_{i-j+3}$.
3. Вычисляем у нее три сингулярных значения (третье будет почти равно 0), и берем правый сингулярный вектор размера 3, который соответствует этому почти нулевому сингулярному значению.
4. Пусть это вектор содержит $a_1, a_2, a_3$, находим корни квадратного уравнения $a_3 x^2 + a_2 x + a_1=0$, они будут комплексными, считаем от каждого корня логарифм, чтобы вытащить фазу, и убеждаемся, что она равна тому, что было задано изначально в самом сигнале.

Должно работать, правда я мог где-то напортачить в обозначениях, и, тогда надо фазу взять с минусом.

[svv]

Schrodinger's cat в сообщении #1565737 писал(а):

svv понятно.
Но в программе это я так понимаю не нужно, у нас уже есть вектор коэффициентов $a$, относительно которого можно построить полином.

Так я же объяснял, откуда берётся алгебраическое уравнение, почему оно именно такое. Я отвечал на Ваш вопрос:

Schrodinger's cat в сообщении #1565630 писал(а):

Но как из разностного уравнения получили степенной... пока недопираю.

Вообще, подчеркну то, что так или иначе надо будет сделать в программе:

svv в сообщении #1565701 писал(а):

Совершенно то же у нас. Сначала мы анализируем длинную последовательность отсчётов и находим, что она удовлетворяет разностному уравнению
$x_{n+4}-13x_{n+3}+69x_{n+2}-197x_{n+1}+260x_n=0$
Или, в наших обозначениях, последовательность $x$ аннулируется оператором
$\mathsf L^4-13\mathsf L^3+69\mathsf L^2-197\mathsf L+260$
Но как из этого извлечь гармоники? Оператор надо разложить на множители вида $\mathsf L-r_k$. Для этого берём (характеристическое) алгебраическое уравнение $r^4-13r^3+69r^2-197r+260=0$, решаем (или, что то же, раскладываем на множители левую часть). Получаем корни
$r_1=4\quad r_2=5\quad r_3=2+3i\quad r_4=2-3i$.
Значит, и оператор допускает разложение
$(\mathsf L-r_1)(\mathsf L-r_2)(\mathsf L-r_3)(\mathsf L-r_4)$
с теми же $r_k$. После этого $\lambda_k=\ln r_k$.

Конечно, если Вы уже нашли коэффициенты в разностном уравнении, Вы прошли 1/3 пути.

[Евгений Машеров]

B@R5uk в сообщении #1565706 писал(а):

Ну, при некоторой ловкости рук Фурье даже меняющуюся частоту переваривает.

Ну, это уже не совсем Фурье. Хотя оно ещё не "топор в солдатском супе". Но только часть расчёта. Выбор окон, выбор весовой функции и ещё много деталей за пределами "чистого Фурье".

[Schrodinger's cat]

svv просто не могу себе представить чтобы эта мелкая программа делала разложение, это же нужен символьный процессор причем далеко не простой. Вы и сами воспользовались ВольфрамАльфа для этого. Явно же так не делают. Руками да, можно упражняться, но в C++/C# явно нет.
Мне кажется я полином неправильно составляю... вечером все перепроверю...

ilghiz в сообщении #1565773 писал(а):

Вот позвольте предложить

На этот раз весьма понятно, спасибо.

[Евгений Машеров]

Фурье не всегда лучший выбор для получения спектра сигнала. Доступный - да. Но создавали Фурье не для этого, а для решения уравнений матфизики.
Как идея, как возможность представлять сигнал не только во временной, но и в частотной области, разумеется, он бесценен. Но вот если оценивать конкретный сигнал...
Прежде всего - мы пытаемся оценить точно, используя для этого столько же параметров, сколько и отсчётов данных. Превращая n действительных отсчётов в $\frac n 2$ комплексных значений. То есть любые ошибки, будь то ошибки измерения, вычисления или помехи, искажающие сигнал, приближаются абсолютно точно. И если рассмотреть задачу оценивания спектра сигнала, отягощённого помехой (ну, скажем, гауссовским шумом постоянной амплитуды), то оценка спектра через Фурье окажется несостоятельной, увеличение длины сигнала точности нам не прибавит. Чем больше отсчётов - тем больше точек в спектре, и на оценку амплитуды данной частоты всё равно только два отсчёта. В предположении гауссовского шума - оценка имеет распределение $\chi^2$ с двумя степенями свободы независимо от длины отрезка. Если мы желаем повысить точность - надо разбивать отрезок на части, считать спектр на каждой (разумеется, по частоте получится загрубление, интервал между частотными отсчётами выше), а потом усреднять спектры частей. Или усреднять соседние отсчёты, соответственно загрубляя спектр.
Ещё одна проблема - реальные компоненты сигнала,по всей вероятности, не будут иметь частоту, точно совпадающую с "зубцами гребёнки". Поэтому у нас будет два пика вокруг настоящей частоты и много мелких, разбросанных по всему спектру. Усреднение по соседним отсчётам борется с этим (как и введение оконной функции, собственно, это эквивалентные подходы, в частотной и временной областях).
Прони, Берг, авторегрессионные и т.п. работают во временной области. Впрочем, можно и в частотной, приближая чем-то вроде $y_t=\Sigma_i A_i\cos(\omega_i t+\varphi_i)$, где частоты и фазовые сдвиги являются параметрами оптимизации (скажем, в смысле минимизации квадратов отклонений), что приводит к нелинейным задачам. Главное преимущество (и главная проблема) что параметров можно взять куда меньше, чем отсчётов, и это позволит оценить их (а для методов во временной области от оцененных параметров перейти к частотному представлению) достаточно точно. При этом оцененные частоты не обязаны принадлежать к заданной сетке частот. А проблема в том, что надо знать число компонент заранее, чтобы выбрать число параметров модели.

[B@R5uk]

Евгений Машеров в сообщении #1565793 писал(а):

Выбор окон, выбор весовой функции и ещё много деталей за пределами "чистого Фурье".

Тем не менее Фурье делает ключевую работу: осуществляет частотное разрешение (расщепление, дифференциацию) сигнала. Всё левое, что на Фурье накручено, призвано лишь добавить несвойственное Фурье временное разрешение. Теоретически, с этим должны вейвлеты справляться. На практике однако же, ещё не придумали такие вейвлеты, чтобы они были одновременно дискретными, легко считались и давали такое же хорошее разрешение по частоте, как и Фурье.

Кстати, окна у меня исключительно такие, чтобы сумма квадратов их последовательности равнялась константе (в моём случае константа равна полтора). Таким образом я получаю обратимость оконного БПФ. При этом, правда, имеется четырёхкратное пересемплирование (в конечном результате один блок сигнала складывается из четырёх Фурье образов-прообразов, сдвинутых относительно друг друга), но за то это позволяет использовать весовую функцию типа "один-ноль" без всяких проблем с гладкостью.

[B@R5uk]

B@R5uk в сообщении #1565802 писал(а):

...чтобы они были одновременно дискретными, легко считались и давали такое же хорошее разрешение по частоте, как и Фурье.

Самое главное забыл: обратимость. А то картинок красивых можно кучу нарисовать с помощью вейвлетов. Вот только какой от них толк, если нельзя обратное преобразование сделать с отредактированному спектру и получить отредактированный сигнал?

[svv]

Schrodinger's cat в сообщении #1565794 писал(а):

svv просто не могу себе представить чтобы эта мелкая программа делала разложение, это же нужен символьный процессор причем далеко не простой. Вы и сами воспользовались ВольфрамАльфа для этого. Явно же так не делают. Руками да, можно упражняться, но в C++/C# явно нет.

Вы меня в какой-то момент перестали понимать. Смотрите: я показывал с помощью WolframAlpha, как, зная $\lambda_k$ (в реальной работе они неизвестны, а в их нахождении и состоит метод Прони), получить полиномиальное уравнение — чтобы Вы понимали, откуда берётся простая связь между $\lambda_k$ и полиномиальным уравнением. То есть всего лишь раскрывал скобки и приводил подобные. И написал, что это гораздо легче, чем обратная операция — решение полиномиального уравнения.

В методе Прони Вам этого делать не надо, а надо идти в обратную сторону:
1) Из отсчётов решением СЛАУ получить коэффициенты полиномиального уравнения (Вы говорите, что они у Вас уже есть).
2) Решить это уравнение, найти его корни $r_k$, а по ним найти $\lambda_k=\ln r_k$.

Я об этом уже писал:

svv в сообщении #1565414 писал(а):

На первом этапе по сигналу находится характеристический полином (осуществляющий то самое линейное предсказание).
Второй этап — определение коэффициентов затухания, сводится к решению одного алгебраического уравнения высокой степени.
На третьем этапе определяются коэффициенты при экспонентах.

svv в сообщении #1565513 писал(а):

На этом и основан метод Прони. А именно, будем действовать в обратную сторону: сначала найдём, какое линейное соотношение с постоянными коэффициентами выполняется для соседних отсчётов (т.е. найдём эти коэффициенты при отсчётах). А потом по коэффициентам восстановим $\lambda_k$.

svv в сообщении #1565530 писал(а):

Чтобы получить коэффициенты линейного разностного уравнения, надо решить СЛАУ. Чтобы по известным коэффициентам восстановить параметры экспонент ($\lambda_k$), надо решить одно алгебраическое уравнение высокой степени (равной числу экспонент).

svv в сообщении #1565701 писал(а):

Оператор надо разложить на множители вида $\mathsf L-r_k$. Для этого берём (характеристическое) алгебраическое уравнение $r^4-13r^3+69r^2-197r+260=0$, решаем (или, что то же, раскладываем на множители левую часть). Получаем корни
$r_1=4\quad r_2=5\quad r_3=2+3i\quad r_4=2-3i$.
Значит, и оператор допускает разложение
$(\mathsf L-r_1)(\mathsf L-r_2)(\mathsf L-r_3)(\mathsf L-r_4)$
с теми же $r_k$. После этого $\lambda_k=\ln r_k$.

[Schrodinger's cat]

Евгений Машеров в сообщении #1565793 писал(а):

"топор в солдатском супе"

Вот топор в солдатском супе.
https://habr.com/ru/post/253447/?ysclid=l8obvi7fz8444876271
Рис.6 наглядная демонстрация.
Да и идея в общем то простая. Детектируем одну гармонику, вычитаем из сигнала, детектируем другую...
Но у меня толком не получилось. Может у Вас (участники темы) получится.

B@R5uk в сообщении #1565812 писал(а):

Самое главное забыл: обратимость. А то картинок красивых можно кучу нарисовать с помощью вейвлетов. Вот только какой от них толк, если нельзя обратное преобразование сделать с отредактированному спектру и получить отредактированный сигнал?

Почему Вы решили что нельзя? Обратные формулы же есть.
Правда прямое вейвлет преобразование у меня получается, разноцветные картиночки. А вот обратное, сколько ни пробовал, фигня. Но я думал проблема в моих кривых руках, и я это отложил в долгий ящик.
Только в вейвлетах такая же проблема возникает, детектирования гармоник.
Что делать если они плавают, сливаются, разделяются...
Ну более менее стационарные удается отлавиливать если построить спектр по масштабам. Экстремумы более менее показывают масштабы гармоник.

[Евгений Машеров]

А что такого сложного с обратными вейвлетами?
https://www.mathworks.com/help/wavelet/ ... hm.html?ue

[B@R5uk]

Schrodinger's cat в сообщении #1565823 писал(а):

https://habr.com/ru/post/253447/?ysclid=l8obvi7fz8444876271

Рис.6 наглядная демонстрация.
Да и идея в общем то простая.

Как по мне это всё ещё детские игры, до практической реализации ещё очень далеко. Да, идея (домножить на комплексную экспоненту, чтобы сдвинуть спектр) простая и в чём-то гениальная, но на одной идее далеко не уедешь.

Первое, что автор статьи не понимает — это то, что нельзя Фурье применять без какой-либо оконной маски. Причём это касается не только реальных сигналов, но и большинства тестовых. Причина этого — граничные эффекты. Дискретный Фурье действует не просто на отрезке, он действует на зацикленном отрезке, фактически на кольце. Поэтому частоты сигнала, не попадающие на "зубцы гребёнки" базиса Фурье (как пишет ув. Евгений Машеров) будут иметь изломы и разрывы на концах отрезка при замыкании его в кольцо. А такие особенности в сигнале имеют широченный спектр (разрыв: затухание $1/f$, излом: затухание $1/f^2$), что и приводит ко всем этим гадостям, с которыми автор статьи пытается бороться с помощью "гетеродинирования". Вот наглядный пример, демонстрирующий этот факт:

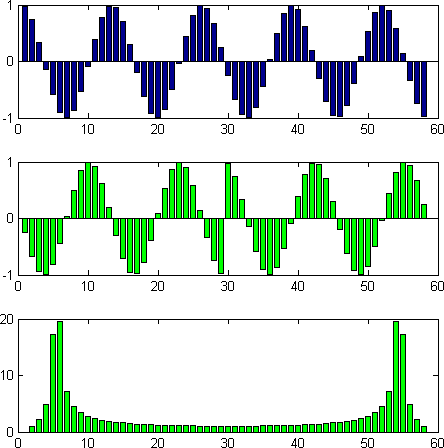
Первый и второй сигналы отличаются лишь циклическим сдвигом вдоль кольца разложения Фурье. В цетре графика второго сигнала явно виден скачок, возникающий на сшивке границ отрезка с первым сигналом. Амплитуды спектров обоих сигналов наложены один на другой на третьем графике. Видно, что они совпадают один в один. И это не удивительно. Циклический сдвиг во временной области меняет только фазу в спектральной области. Демонстрационный код:

Используется синтаксис Matlab M

clc
clearvars
format compact

num = 58;
xx = ((1 : num)' - 0.5) / num;

yy1 = cos (2 * pi * xx * 4.5);
yy2 = [yy1(num / 2 + 1 : end); yy1(1 : num / 2)];

subplot (311)
bar (yy1)
subplot (312)
bar (yy2, 'g')
subplot (313)
bar (abs (fft (yy1)))
hold on
bar (abs (fft (yy2)), 'g')
hold off
 

Второй факт, который не понимает автор статьи, заключается в том, что реальные сигналы (как я уже неоднократно писал выше) всегда имеют плавающую частоту/фазу и изменяющуюся амплитуду. На практике это сводит на ноль всё, что автор в статье делает. Ну просто потому, что любой реальный сигнал будет иметь широкий спектр в несколько линий. Именно в этих нескольких соседних линиях зашифрованы те плавающие амплитуды и частоты, которые в сигнале наблюдаются (смотрите мой первый пост на этой странице, например). Чем быстрее (со временем) эти изменения происходят, тем больше информации хранится в одной гармонике, тем шире её спектр (очень логично, не находите?). По этой причине вырезание одной гармоники из спектра реального сигнала — это всегда вырезание нескольких спектральных линий.

Оконные функции решают как первую проблему, так и помогают с решением второй. В гетеродинировании отпадает надобность. Да, умножение сигнала на оконную функцию уширяет спектр на две линии (всего!!!), но, поскольку реальный сигнал уже широкий, это оказывается не страшно. А "лепестки" оконных функций как правило безвозвратно тонут в фоновом шуме, который естественным образом присутствует в реальном сигнале.

-- 30.09.2022, 15:27 --

Евгений Машеров в сообщении #1565831 писал(а):

А что такого сложного с обратными вейвлетами?

Конкретно с теми, что вы привели — неудовлетворительное спектральное разрешение. Вообще, если вы хотите мне помочь понять, какие именно вейвлеты мне нужны, добро пожаловать в отдельную тему. Если действительно получится достичь хоть какого-то практического результата, буду несказанно благодарен!

[Евгений Машеров]

Помнится, некогда делали "очистку" звука, вейвлет-преобразованием (и как бы не Хаара), домножением коэффициентов $a_i$на $\frac {a_i^2}{a_i^2+k}$, где k - подбираемый параметр (со смыслом - дисперсия шума в расчёте на отдельный вейвлет) и обратное. Вроде как работало...

[Schrodinger's cat]

Не знаю, ничего не работает.
Посмотрите пожалуйста листинг программы, старался оформить максимально понятно.
Файлы mathcad'a у кого есть, прайм. Тоже самое pdf.
Все это писать сюда ЛаТексом я умру.
https://disk.yandex.ru/d/TNfQNemTGa9vig
Classic - Соответственно исходный метод Прони.
SVD - как писал ilghiz.

ПС: Чувствую себя идиотом
Хотя не так давно Фурье прямое, обратное, трансформацию Гильберта через Фурье, прямой Вейвлет освоил относительно без заморочек. Совсем недавно освоил разложения QR четырьмя методами, SVD двумя методами вообще без помощи кого либо... Может не стоило приходить на форум