Добрый вечер! Есть решение, хотелось бы разобраться с ним, помогите, пожалуйста!
Задача такая:
В строку подряд написано

чисел. Под каждым числом

первой строки напишем число, указывающее, сколько раз число

встречается в первой строке. Из полученной таким образом второй строки аналогично получаем третью: под каждым числом второй строки пишем, сколько раз оно встречается во второй строке. Затем из третьей строки так же получаем четвёртую, из четвёртой — пятую, и так далее.
1) Докажите, что

‐я строка совпадает с

‐й.
2) Приведите пример такой первоначальной строчки, для которой

‐я строка не совпадает с

‐й.
Решение.
Докажем, что если в m-ой строчке при

, число отлично от написанного над ним, то оно не меньше, чем

.
Действительно, для

это очевидно, так как все числа второй строки натуральные. Пусть это уже проверено для всех строк с номерами, меньшими

. Пусть в

-ой строчке написано число

, а под ним написано число

. Тогда в

-ой строчке написано

чисел, равных

. Ясно, что в

-ой строчке будет написано несколько групп одинаковых чисел, по

в каждой группе, причем числа из разных групп различны. Отсюда вытекает, что

делится на

, то есть

. Кроме того, по крайней мере одно из чисел в этих группах отличается от

, а значит, по предположению индукции

. Итак,

. Наше утверждение доказано по индукции для всех

. Если предположить, что

-я строчка отлична от

-й, то какое-то число в

-й строчке будет больше, чем

, что невозможно.
В оффтопе оригнал решения:
(Оффтоп)
Я большую часть решения понял, кроме двух фраз:
1)
Цитата:
Ясно, что в

-ой строчке будет написано несколько групп одинаковых чисел, по

в каждой группе, причем числа из разных групп различны. Отсюда вытекает, что

делится на

Допустим у нас есть несколько групп чисел, по

в каждой, причем различных (кстати, а если

)?
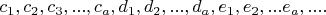
Но как отсюда следует, что

делится на

?
2) Почему обязательно найдется

(в самом начале рассуждения)?



