Интересно есть ли какие-то подвижки в доказательствах ограничения

сверху, тоже как-то всё затихло. Причём без подведения итога, что доказано, что не очень, а что совсем нет.
Я вот тут недавно практически случайно "передоказал" (с помощью вольфрамальфа) что для цепочек длиной от 10 и более с 12-ю делителями невозможны варианты

, все такие цепочки имеют или составное

или составное

на месте

(а вариант

вообще целых решений не имеет). В частности это сразу снова ограничивает

и требует во всех таких цепочках (длиной от 10 и выше) число вида
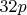
.
Вот почему некоторые так любят принимать вопросы за предложения или требования? Вот почему некоторые, не увидев расчётов или прикидок, считают что их вовсе нет?
Т.е. прикидки у Вас есть? И сколько там выигрыш? И почему не сказать об нём сразу? А раз не сказали то и делаю вывод что не прикидывали.
Я пока даже не представляю как исключить из проверок одно из простых. Вроде бы достаточно потребовать чтобы оно не попадало в цепочку длиной 15, т.е. из скажем 37 вариантов размещения простого 37 кроме 9-11 уже и так запрещённых (попадает на проверяемое место) добавятся ещё 4-6 вариантов и их станет не 9-11, а ровно 15. 9-11 вариантов дают выигрыш скорости в

раза, 15 вариантов дадут выигрыш в

раза, на 18%-27% больше. Т.е. работа ускорителей ускорится процентов на 20. Немного.
Но для простого 31 ускорение составит до 37%, для 29 до 43%, для 23 до 75%, для 19 до 150%, для 17 до 300%. Да, вот это уже интересно.
Осталось понять правильно ли я подсчитал и получится ли реально такой выигрыш или так делать нельзя.
Кстати я тут подумал, выше Вы где-то предлагали считать вторую таблицу по строкам подставляя в неё одно из выброшенных чисел, я смысла в этом не увидел (ведь подставлять придётся все простые до миллиона с чем-то), фактически это превращает её в первую таблицу, только 5-е простое не 17...37, а больше. И пока счёт по строке первой таблицы с таким подставленным простым занимает существенно больше нескольких часов (т.е. заметно превышает время компиляции) может и имеет смысл так считать, во всяком случае для подставляемых простых до нескольких сотен (пока общее время просчёта всех вариантов сильно меньше времени просчёта строки второй таблицы).
Менять программы при этом не нужно, достаточно лишь правильно инициализировать массив rr[] в последней версии генератора паттернов M12mods1.gp (rr[6]=1 и ещё одно значение из rr[1..5] заменить на новое простое большее 37, но до 180 чтобы не сбилась нумерация паттернов).
-- 08.09.2022, 10:03 --На настоящий момент рекордная непрерывная 14-ка

находится на 25-м по величине месте среди всех 14-к. Такую длинную таблицу конечно постить не буду,
Считаю напрасно, ну тогда выложу свою версию этой таблицы до текущей проверяемой границы, под катом:
(Оффтоп)
S9-32-204531:3797306190383689322319167788441: 12,128, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
S9-43-204103:8465690351577098126087841014041: 12, 4, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
N9-73-421506:259037697563588532195140710301145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, valids=14, maxlen=12, ALL
S2-46-503162:517323644441352164508238287911641: 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
S9-26-536401:937749576115599672133078413902041: 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
S9-41-503214:1644045397000202097257384783236441: 12, 32, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13
S9-51-345102:2523070846505196118004730922674841: 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
N9-42-210436:2596570872606845562606814561185945: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 4, 12, 12, 12, 12, valids=14, maxlen=10
S9-45-601425:3067156509258374440567582835178841: 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
N2-46-062134:3622442787032728972968170496168345: 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13
N9-46-062134:5647219565443862443036265765544345: 12, 12, 4, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=12, ALL
N9-41-601432:5675649020130167140192706236675545: 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
N9-42-601532:5831310458930984039881054111185945: 12, 12, 12, 12, 12, 12, 96, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
S2-36-203164:6107879360323054060768953285196441: 12, 24, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13
N9-42-104523:6523980598256304645405510380073945: 12, 12, 12, 12, 12, 12, 16, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
N2-35-521043:7366533154797877735424335147176345: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, 12, valids=14, maxlen=12
S9-53-532401:8527821822518768120123764664174041: 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
N2-45-652403:9687936215599602783812822055365145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, valids=14, maxlen=13, ALL
S9-51-532041:9922985334352780337966587369910041: 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
S9-45-405621:9934168307077120855717822079092441: 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
N9-26-624013:10450183440390298033961001751872345: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 4, 12, 12, 12, 12, valids=14, maxlen=10
N9-53-361204:10811479606888915408182631166097945: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 64, 12, valids=14, maxlen=13
N9-23-152046:10971860581411131970471492130193945: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, valids=14, maxlen=12, ALL
S9-56-530412:11590620189478148425607728011724441: 12, 12,128, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=12
S9-21-231054:11802394069079756844950115237998041: 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
N2-51-623410:11865604480910140781102260713619545: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 2, valids=14, maxlen=14, ALL, 14!
N2-34-543210:12641644871583861275062199467757145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 64, valids=14, maxlen=14, ALL, 14!
S2-24-305142:13525803452264068006389357653466841: 12, 32, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13
S9-25-206134:14128103842834262705098540251398041: 12, 16, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13
S2-24-045213:14338620420493961557283066155430041: 16, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=14, ALL, 14!
S9-45-403215:15214478487016103814314590531002841: 12, 64, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13
N2-41-056214:15469076928116388660262145780971545: 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
S9-41-120346:15827288908604089755802588633890841: 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=10
N2-36-216405:16556872878417124149541186173893145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, valids=14, maxlen=13, ALL
N9-24-023145:17273405686929167369087359819051545: 12, 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=12, ALL
N9-31-406321:18115721284075070458231413462365145: 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8
N9-23-432610:23466238381659111718270264154333145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 4, valids=14, maxlen=14, ALL, 14!
N2-34-542016:29610306012832880625063323461680345: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, 12, valids=14, maxlen=12, ALL
N9-54-160425:34087264745107069755813968843309145: 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
S9-42-413650:35909988261042170071773296516524441: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, valids=14, maxlen=12, ALL
N9-52-350416:40746184981866946200175530669283545: 12, 12, 12, 12, 12, 12, 12, 12, 8, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
N9-23-365041:44329553754851817207515067762105945: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, valids=14, maxlen=12, ALL
S9-41-206541:45456300823830261034040795069327641: 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
N9-46-541260:49735258463353263039592853384529945: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12,256, valids=14, maxlen=14, ALL, 14!
N9-23-031624:51322750844692191384510458114899545: 12, 12, 8, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=12, ALL
S9-26-215406:56604455756596920521899453890244441: 12, 12, 12, 12, 12, 12, 12, 12, 16, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
N2-53-042561:61945393977471830074151699168549145: 12, 16, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=13, ALL
N9-21-052416:65361244491031342864913813024073945: 12, 12, 12, 12, 12, 12, 32, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
S9-52-164052:73374588290748365254417551462350041: 12, 12, 12, 12, 12, 12, 16, 12, 12, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
N9-42-521640:79530036533832633126783680099285145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 16, valids=14, maxlen=14, ALL, 14!
N2-56-354126:81208614941517230882469765804509145: 12, 12, 12, 12, 12, 12, 12, 12, 24, 12, 12, 12, 12, 12, 12, valids=14, maxlen=8, ALL
S9-36-587241:97648097903866012734106659998399641: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, valids=15, maxlen=15, ALL, FOUND!!!