мы не можем посчитать векторное произведение в сферических координатах
Векторное произведение в сферических координатах вычисляется с помощью формул (где
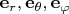
— это
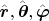
):
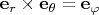
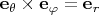
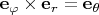
Плотность тока и радиус-вектор имеют только компоненты

поэтому их векторное произведение только компоненту
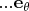
. Нюанс в том, что в каждой точке пространства свой локальный базис
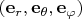
. Поэтому вектор
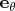
в подинтегральной функции не является константой, и его нельзя вынести за знак интеграла. Однако ясно, что в силу осевой симметрии векторный результат интегрирования будет направлен по оси

. Поэтому можно интегрировать не векторную функцию с зависящим от точки
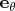
, а её проекцию на ось

, воспользовавшись формулой
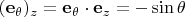
Альтернативный способ — выразить
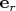
и
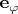
через декартовы орты с помощью
формул перехода, потом взять векторное произведение в декартовых координатах и опять оставить только компоненту

. По-моему, так чуть сложнее.
Кстати, обратите внимание, что в формуле Био-Савара-Лапласа вектор, обозначенный у Вас

, направлен из точки, где течёт ток, в точку, где вычисляется поле. А радиус-вектор

, наоборот, направлен из начала координат (где надо найти поле) в точку, где ток. Если это учесть, «минуса» в ответе не будет.