Пятно Пуассона

[Middle]

Согласно теории Пуассона и экспериментальным данным, в точке $P$ (центра геометрической тени диска) будет образовываться яркое пятно.

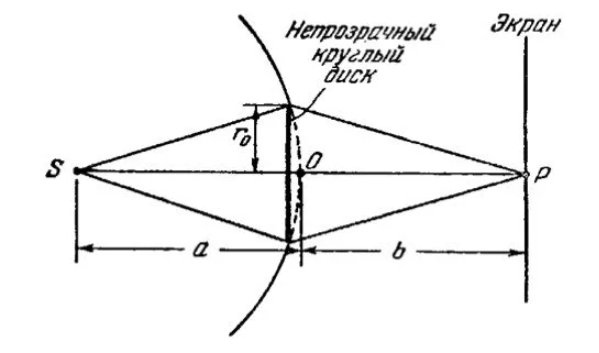
Понятно, что это можно показать через диаграммы Френеля(потому как диск перекрывает не все, а только $n$ зон френеля)
Ну а что если разместить экран несколько дальше от точки $P$ или несколько ближе к точке $O$.
В силу произвольности $b$ в новой точке $P'$ тоже будет яркое пятно.
Выходит, что мы можем видеть яркий луч $OP?$(Потому как было бы странно, если бы эти пятна $P'$ зависели от присутствия экрана на соответствующем расстоянии $b'$)