Насколько реальна гипотеза для A091892?

[kthxbye]

Пусть $a(n)$ это A091892.

Пусть

• $\left\lbrace c(n)\right\rbrace$ это подпоследовательность $\left\lbrace b(n)\right\rbrace$
• $\left\lbrace d(n)\right\rbrace$ это подпоследовательность $\left\lbrace b(n)\right\rbrace$

Тогда мы имеем следующую гипотезу:

• объединение $\left\lbrace c(n)\right\rbrace$ и $\left\lbrace d(n)\right\rbrace$ это $\left\lbrace a(n)\right\rbrace$

Гипотеза была проверена до $a(764)$, т.е. до максимального члена в б-файле, прикрепленном к последовательности.

Можно также убедиться, что $\left\lbrace c(n)\right\rbrace$ и $\left\lbrace d(n)\right\rbrace$ не имеют общих членов (проверено до $d(2^{14})$).

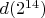
Теперь о том, кто же у нас такие $b(n), c(n), d(n)$.

Последовательность $\left\lbrace b(n)\right\rbrace$ это числа $k$, такие, что A007814$(k+1)>$ A086784$(k+1)$ с добавлением $b(0)=0$.

Чтобы получить члены последовательности $\left\lbrace c(n)\right\rbrace$, используйте следующее правило: $b(n)$ является членом в том случае, если $e(n)=1$. Также $c(0)=0$.

И, наконец, $\left\lbrace d(n)\right\rbrace=\left\lbrace 128d_1(n)-1\right\rbrace$.

Здесь $e(n)=1-e_1(s(n))$, где $\left\lbrace s(n)\right\rbrace$ это A280514 с добавлением дополнительной единицы в начале, т.е. $s(1)=s(2)=1$, $s(3)=2$ и т.д.

В свою очередь, $e_1(n)$ принадлежит $\left\lbrace0,1\right\rbrace$. Члены задаются так:

• при $n<55$ у нас $e_1(n)=1$ при $n = 13, 18, 20, 26, 28, 31, 34, 39, 41, 44, 47, 49, 52, 54$. Что примечательно, это члены A001950 с индексами от 5 до 19 с исключением членов с индексами 6, 9 и 14.
• при $n\geqslant55$ имеем:
• в представлении Зекендорфа для $n$, если каждый бит это единица минус предыдущий, то $e_1(n)=1$.
• в представлении Зекендорфа для $n$, удалите один бит равный нулю в крайней слева последовательности нулей с длиной больше единицы и вернитесь обратно к десятичному представлению с результатом $m$. Тогда $e_1(n)=e_1(m)$.

Также $\left\lbrace d_1(n)\right\rbrace$ это числа $k$, такие, что $f(k)=1$. Здесь $f(n)$ принадлежит $\left\lbrace0,1\right\rbrace$. Члены задаются так:

• если $n$ четное, то $f(n)=f_1(\frac{n}{2})$.
• если $n$ нечетное, больше единицы и второй слева бит в двоичном представлении $n$ равен нулю, то $f(n)=f_1(n)$, в противном случае ноль.

Наконец $f_1(n)$ принадлежит $\left\lbrace0,1\right\rbrace$ и задается так:

• при $n<18$ у нас $f_1(n)=1$ при $n=17$
• при $n\geqslant18$ имеем:
• если $n$ четное, то $f_1(n)=f_1(\frac{n}{2})$.
• если $n$ нечетное и число единиц двоичной записи $n$ больше двух, а $m$ это позиция второго крайнего справа бита, то $f_1(n)=f_1(\frac{n+1}{2}-2^{m-1})$, в противном случае ноль.

На этом, собственно все (т.е. все задано).

Имеет ли эта гипотеза право на существование? Верна ли она также для больших $n$? Чем можно объяснить участие той или иной вспомогательной последовательности?

Вот вам еще программка на PARI для проверки:

default(parisizemax,2^8*10^6) 
q1(n)=2^valuation(n,2) 
q2(n)=n\(2*q1(n)) 
fib1(n)=local(m); if(n<1, 0, m=0; until(fibonacci(m)>n, m++); m-2) \\ A072649 
fib2(n)=n-fibonacci(fib1(n)) 
fib3(n)=n>2*fib2(n) 
Zeckendorf(n)=my(k=0, v, m); while(fibonacci(k)<=n, k=k+1); m=k-1; v=vector(m-1); v[1]=1; n=n-fibonacci(k-1); while(n>0, k=0; while(fibonacci(k)<=n, k=k+1); v[m-k+2]=1; n=n-fibonacci(k-1)); v 
g(n)=fibonacci(fib1(n)+2)-n 
h(n)=if(n==1,1,my(A=fib1(n-1), B=2^A, C=n-1, D); for(i=1, A, B+=(1-fib3(C))*2^(A-i); C=fib2(C)); B+1) \\ A353654 
b(n)=(q2(h(n+1))+1)*q1(h(n+1))-1 
isok1(n)=if(n<55,n==13 || n==18 || n==20 || n==26 || n==28 || n==31 || n==34 || n==39 || n==41 || n==44 || n==47 || n==49 || n==52 || n==54,my(A=Zeckendorf(n), A1=Vecrev(A), B, C=1, D=0); B=sum(k=1,#A\2,A[2*k-1]==1 && A[2*k]==0)==#A\2; B=if(#A%2, B*A[#A], B); if(B==0, until(A[C]+A[C+1]==0, C++); D=isok1(sum(k=1,#A-C,A1[k]*fibonacci(k+1))+sum(k=#A-C+2,#A,A1[k]*fibonacci(k)))); B+D) \\ e1(n) 
isok2(n)=1-isok1(g(n)) \\ e(n) 
isok3(n)=if(n<18,n==17,my(A=0, B=0, C=0); if(n%2==0, A=isok3(n/2), if(hammingweight(n)>2, until(bittest(n,B)==1, B++); C=isok3((n+1)/2-2^(B-1)))); A+C) \\ f1(n) 
isok4(n)=if(n%2==0, isok3(n/2), if(n>1 && binary(n)[2]==0, isok3(n))) \\ f(n) 
isok5(n)=if((n+1)%128==0,isok4((n+1)/128)) 
upto=2^10; v=vector(upto,i,0); x=0; z=1; z1=0; while(x<upto, while(!(isok2(z)), z++); x++; v[x]=b(z); if((b(z)+1)%128==0 && x+1<upto, z1=z+1; while(!(isok2(z1)), z1++); for(i=z+1,z1,if((b(i)+1)%128==0 && isok4((b(i)+1)/128), x++; v[x]=b(i);))); z++); \\ a(n) 
print(v) 
\\z=1; z1=1; for(k=1, 299, while(!(isok5(z)), z++); until(b(z1)==z, z1++); print(isok2(z1)); z++; z1++); \\ проверка что у c(n) и d(n) нет общих членов