Теормех. Кол-во неизвестных превышает число уравнений

[Middle]

Условие задачи: Ползун $B$, перемещаясь по горизонтальной направляющей по закону $s_{B}(t)=0,01t^2+0,18t$, приводит в движение через шатун $AB$ колесо радиуса $R=0,1$ м . Колесо катится по горизонтальной плоскости без скольжения.
В момент времени $t=1$ с опеределить скорости и ускорения точек $A$ и $C$, если в этот момент механизм занимает положение указанное на рисунке:


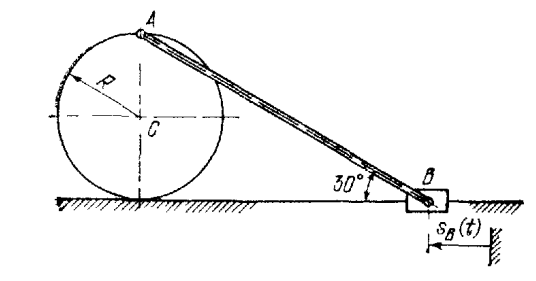
Понятно, что скорости в колесе будут распредлены следующим образом



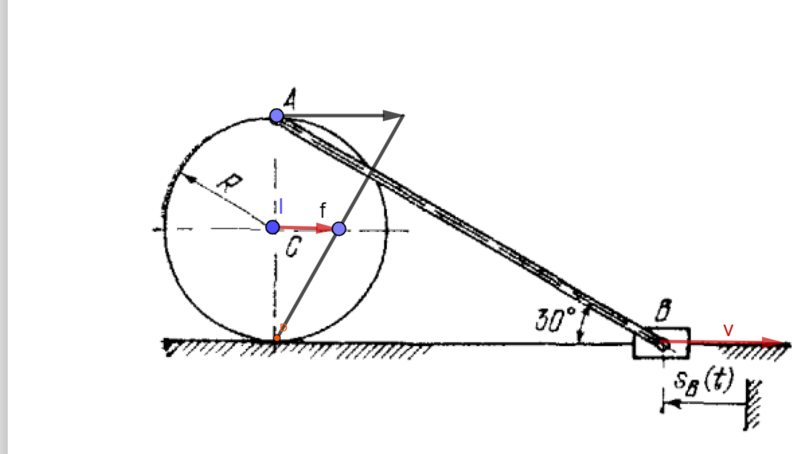
А движение стержня будет мгновенно поступательным.
Тогда запишем формулы эйлера:

$W_{A}=W_{B}+[\varepsilon_{AB}\times AB]$

$W_{A}=W_{C}+[\varepsilon_{K}\times AB]-\omega_{K}^2 \cdot \vec{CA}$

Где $\omega_{K}$, $\varepsilon_{K}$ - Угловая скорость и угловое ускорение колеса

Поскольку м.ц.с колеса-точка соприкосновения колеса и плоскости (точка $D$), то, записав ур-е скорости для точки $A$, получим:

$V(t)_A=V_{D}+[\omega(t)_{K}\times DA]=\omega_{K}(t)\cdot DA$

$\omega_{K}(t)=\frac{V(t)_A}{DA}$ , $V(t)_{A}=S'(t)$

$\varepsilon_{K}=\omega'_{K}(t)$

И дальше остается вернуться к двум формулам для ускорения точки $A$ и понять, что последнюю невозможно найти:
Для этого нужно знать угловое ускорение стержня $AB$ или ускорение точки $C$(или $D$), или углы наклона вектора $W_{A}$ к осям.
Подскажите, как продвинуться в решении этой задачи

[EUgeneUS]

запишите уравнение кинематической связи, которое свяжет угол поворота колеса и координаты точки $B$. И продифференцируйте два раза.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- придумайте более информативный заголовок;
- все-таки наберите текстовую часть условия в виде текста, а в виде картинок оставьте только картинки, имеющие непосредственное отношение к задаче.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (Ф)»

[rascas]

С задачей всё нормально. Задача решается.

Middle в сообщении #1561659 писал(а):

$\varepsilon_{K}=\omega'_{K}(t)$

Применение этой формулы в этой задачи ненужно, так как неизвестна зависимость $\omega_{K}$ от времени.

1) Почему Вы выбрали направление скорости $V_B$ вправо?
По чертежу и формуле положительное перемещение $S_B$ влево, $V_B$ и $W_B$ направлены влево. На мой взгляд ни к чему путать себя в этой задаче.

2) Вы знаете направление ускорений в точках $C$ и $D$ ($W_C$ и $W_D$)? Какое оно?

3) Начните с определения ускорения $W_A$.
Примените формулу Ривальса для стержня и для колеса, для вычисления ускорения их общей точке $A$.
Начертите векторы всех слагаемых ускорений из формул Ривальса для стержня и колеса в точке $A$.

4) Далее находим угловое ускорение колеса $\varepsilon_{K}$ и ускорение $W_C$