Известна асимптотическая оценка суммы

, где

- простое число.
Надо определить асимптотическую оценку для более общего случая

, где

- натуральное число.
Хотелось бы используя только теоремы из А.А. Бухштаб "Теория чисел". Я, к сожалению, не знаю, как это сделать.
Попытка решения задачи без использования этого учебника.
Пусть

, если

- простое число и
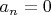
в противном случае. Обозначим

, где

- количество простых чисел, не превосходящих

.
Если

- существует и непрерывна, то используя формулу Абеля к сумме

получим:

.
Так как в данном случае

, то получим:

. (1)
На основании асимптотического закона простых чисел:

. (2)
Подставим (2) в (1) и получим общую формулу:

. (3)
Подставим в (3)

:


. (4)
Учитывая, что:

, (5)
то подставляя (5) в (4) получаем:


Таким образом:
