Ничего несимметричного нету: содержательными оба понятия становятся (как правило) при условии дифференцируемости функции
Несимметричность в том, что при отсутствии дифференцируемости, но существовании всех частных первого порядка, матрица Якоби вполне может существовать, а градиент (если использовать то его определение, которое я написал выше) – нет. То есть если использовать определение из первого поста, то при отсутствии дифференцируемости функции

в точке

вектор из частных производных

первого порядка в принципе нельзя называть градиентом. И это напрягает.
Еще забавный факт – в статье английской википедии с названием
Gradient тоже требуется дифференцируемость функции в точке для существования ее градиента в этой точке: он определяется там фразой "the gradient of a scalar-valued
differentiable function

of several variables is ...". Однако, если открыть в английской википедии статью
Jacobian matrix and determinant, то там определение матрицы Якоби не требует дифференцируемости функции в точке, и это сказано явно: "If a function is differentiable at a point, its differential is given in coordinates by the Jacobian matrix. However a function does not need to be differentiable for its Jacobian matrix to be defined, since only its first-order partial derivatives are required to exist." При этом сама матрица Якоби определяется как набор из градиентов вида

, where

is the transpose (row vector) of the gradient of the

component.
То есть в этой статье уже подразумевается, что градиент

представляет из себя просто вектор из частных производных первого порядка функции

, вовсе не предполагающий дифференцируемость этой функции в точке

.
Наконец, порывшись на math.stackexchange, я нашел там
тему шестилетней давности, где обсуждался аналогичный вопрос, и тамошнее сообщество больше склоняется к тому, что вектор из частных производных первого порядка можно называть градиентом, даже если функция не дифференцируема в точке. Но однозначного консенсуса там нет.
-- Вс июн 26, 2022 16:13:26 --Но на этот источник все равно хотелось бы посмотреть.
Как пожелаете. Отмечу, что курсы лекций и учебники, перечисленные ниже, довольно хорошие, то есть каких-то существенных косяков и опечаток в них мною замечено не было.
1. Дымарский Я.М. Лекции по математическому анализу. Часть II. МФТИ, 2021, страница 162 в середине:
Цитата:
Дифференцируемость равносильна существованию градиента.
2. Иванов Г.Е. Лекции по математическому анализу. Часть 1. МФТИ, 2017, страница 186:
Цитата:
Из существования частных производных по всем переменным не следует дифференцируемость, а значит, не следует существование градиента функции.
3. Бутузов В.Ф. Лекции по математическому анализу. Часть II. Физический факультет МГУ, 2014, страница 38 (это довольно популярный учебник, где отдельно выписано строгое определение градиента и в нем указано, что функция должна быть дифференцируема в точке):
Цитата:
Определение. Градиентом дифференцируемой функции
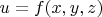
в точке

называется вектор

...
Зорич В.А. Математический анализ. Часть I. МЦНМО, 2002, страница 518. Там градиент функции

в точке

определяется через дифференциал

по формуле

. Естественно, существование дифференциала предполагает дифференцируемость функции в точке

.