Пусть

- это
A340251, индекс бита который был инвертирован в
A340250
для получения
A340250
.
Также пусть

и

Здесь

- это

-й справа бит в двоичном представлении

.
Введем трансформацию для

, такую, что мы начинаем с

и далее присваиваем

для
![$i=[0,\ell(n)-1]$ $i=[0,\ell(n)-1]$](https://dxdy-01.korotkov.co.uk/f/8/6/3/86331cf6ec5be57062252c1c250821ca82.png)
. Вот простейшая программка на PARI для этого:
Код:
b(n)=my(A=n); for(i=0, logint(n, 2)-1, A+=2^i*bittest(A, logint(n, 2)-i)); A
Тогда последовательность, возвращающая результат трансформации - это

.
Пусть
 Гипотеза
Гипотеза: если разбить последовательность
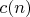
на блоки с длинами

, то каждый блок содержит числа от

до

.
Если для каждого такого блока взять обратную перестановку и совместить все блоки опять в последовательность, то мы получим

.
Гипотеза:

.
Проверить можно так:
Код:
b(n)=my(A=n); for(i=0, logint(n, 2)-1, A+=2^i*bittest(A, logint(n, 2)-i)); A
c(n)=(b(2*n) - 2*n + 1)/2
for(i=0, 8, z=2^i+1; for(j=1, 2^i, while(!(c(z)==j), z++); print1(logint(z-2^i, 2), ", "); z=2^i+1); );
Или вот так:
Код:
b(n)=my(A=n); for(i=0, logint(n, 2)-1, A+=2^i*bittest(A, logint(n, 2)-i)); A
c(n)=(b(2*n) - 2*n + 1)/2
n=9
v=vector(2^n,i,0)
for(i=0, n-1, for(j=1, 2^i, v[2^i+c(2^i+j)]=logint(j, 2)))
print(v)
Можно ли как-нибудь доказать эти гипотезы (или хотя бы одну из них)?



