Зонные пластинки

[profilescit]

Ниже представлена задача которую я решил частично, однако не совсем понял собственное решение. Хотелось бы понять почему то что я делал - правильно и как решить оставшуюся часть задачи. Буду признателен за помощь.


На рисунке (a) показана непрозрачная перегородка, в которой проделано небольшое круглое отверстие радиусом $OM =1.00$ мм.
В качестве источника света используется водородно-неоновый лазер с длиной волны $\lambda=632.8 $нм, параллельный пучок света которого падает на отверстие слева. Справа на оси симметрии отверстия находится точка $P$. Волну в этой точке можно рассматривать как комбинацию волн от полуволновых зон. Обозначим $r_0 = PO$, тогда сферы с центром в точке $P$ радиусами $r_0+\frac{\lambda}{2}$,$ r_0+2 \frac{\lambda}{2}$, $r_0+3\frac{\lambda}{2}$, … разбивают отверстие на $N \in \mathbb{N}$ колец. Расстояние от точки $P$ до края отверстия $M$ равно $r_0+N \frac{\lambda}{2}$, а кольцо с наименьшим радиусом представляет собой круг. Каждое такое кольцо называется полуволновой зоной, поскольку разность оптический путей от его краёв до точки $P$ равна $\frac{\lambda}{2}$. Ясно, что количество зон $N$ определяется положением точки $P$.



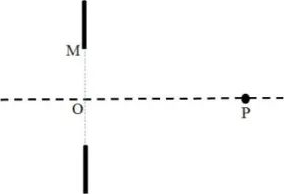
1. Если $N = 2n+1$, найдите расстояние $r_0$ до точки $P_0$ ($P_0$ — крайняя справа яркая точка, называемая главным фокусом) и расстояние $r_1$ до точки $P_1$ ($P_1$ — тоже яркая точка, располагающаяся левее $P_0$, называемая вторичным фокусом).


Пусть теперь $N = 4$, и в первой и третьей волновых зонах помещён прозрачный материал, при прохождении через который оптический путь света увеличивается на $\frac{\lambda}{2}$ (см. рисунок (b)).



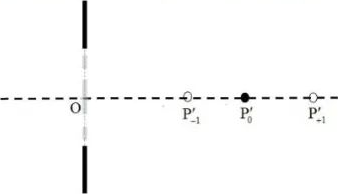
2.1 Найдите расстояние $r_0^'$ до главного фокуса $P_0^'$ такой пластинки.

2.2 Найдите расстояние $r_{-1}^'$ до вторичного фокуса $P^{'}_{-1}$, находящегося непосредственно слева от главного.

2.3 Найдите расстояние $r_{+1}^'$ до вторичного фокуса $P_{+1}^'$, находящегося непосредственно справа от главного.

Зонную пластинку можно использовать не только для фокусировки света, но и для формирования изображения. Рассмотренный выше процесс фокусировки параллельного пучка эквивалентен ситуации, когда предмет находится на бесконечности, а расстояние до изображения равно фокусному. Пусть теперь точечный источник света расположен слева от $O$ на расстоянии $s = 3$ м в точке $S$ на оси симметрии. Как показано на рисунке (c), его изображение обозначим $S^′$.



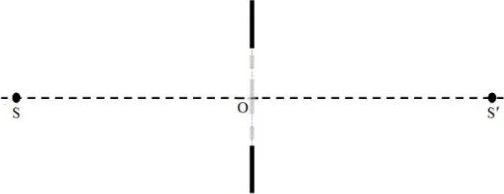
3.1 Найдите $O S^′$, соответствующее главному фокусу зонной пластинки. Справедлива ли формула тонкой линзы?

3.2 Если пластинка формирует несколько изображений, на каком расстоянии $s^′$ от $O$ формируется изображение, ближайшее к рассмотренному в предыдущем пункте? Чему равно фокусное расстояние $f^′$ соответствующего вторичного фокуса (формула тонкой линзы неприменима)?

3.3 Если предмет расположен слева от зонной пластинки на расстоянии $\frac{O P_0^{'}}{2}$ от точки $O$, найдите расстояния $s_1$ и $s_2$
до главного и вторичного изображений, соответствующих фокусам, рассмотренным в предыдущем пункте (формула тонкой линзы также неприменима). Действительные они или мнимые?



И собственно мое решение:

1. Пусть $OM = r$ тогда

$$r_0^2 + r^2 = \left( r_0 + N \frac{\lambda}{2} \right)^2$$

Откуда получим что $r_0 (n) = \frac{r^2}{(2n+1) \lambda} - \frac{(2n+1) \lambda}{4}$
Это монотонно убывающая функция от $n$, тогда $r_0 = r_0 (0) = 1580$ мм и $r_1 = r_0 (1) = 527$ мм что сходится с ответом.

2. Теперь, в зависимости от четности проходимой зоны, разность хода может увеличится на половину длины волны.

Я записал это как $r_0^2 + r^2 = \left( r_0 + N \frac{\lambda}{2} + \delta \frac{\lambda}{2} \right)^2$ где $\delta = 0$ для четных $N$ и $\delta = 1$ для нечетных $N$.

Тогда получим $r_0 (N) = \frac{r^2 - \left( N \frac{\lambda}{2} + \delta \frac{\lambda}{2} \right)^2}{N \lambda + \delta \lambda}$


И тогда получим что $r_0 (1) = r_0 (2) = 790$ мм, $r_0 (3) = r_0 (4) = 395$ мм. В ответе $r_{+1}^{'} = 790$ мм и $r_0^{'} = 395$ мм. Ответ же для r_{-1}^' получается для $r_0 (7) = r_0 (8) = 198$ мм, но непонятно, ведь у нам всего 4 зоны, откуда и как получить такой результат?

Хочу в первую очередь разобраться с этим вопросом и приступить к обсуждению следующих.