Полагаю, что и я и Dmitriy40 стараемся в том числе и тщательно рассматривать Ваши наработки по задаче с разных сторон и под увеличительным стеклом, в надежде хоть как-то уменьшить перебор и/или увеличить его скорость. Плюс исследуются и другие подходы.
Не то чтобы я рассматривал наработки, мне интереснее самому разобраться. И после этого переписать на нормальном языке с глубокой оптимизацией под скорость.
Пока ни одна из моих идей толку не дала, остаётся оптимизировать линейный перебор

(или

как у
VAL, что одно и то же). О первой попытке я уже
писал, оно работает, но есть и следующая мысль: полностью отказаться от умножений и делений и переходить к следующему

одновременным вычислением всех интересующих остатков по малым простым. Это делается лишь сложениями (и сравнениями), которые во первых весьма быстры, во вторых все числа малы по величине, и в третьих потому позволяют задействовать AVX — и ориентировочно в среднем за 10 тактов получать факт делимости 400 чисел на малые модули, например проверить делимость 10-ти чисел на 40 первых простых, т.е. эффективно исключить огромное множество точно неподходящих вариантов со скоростью порядка 300млн/с (

в час). Замечательно что при этом величина самих чисел вообще не важна, все операции кроме начальной настройки производятся в поле (кольце?) модулей. Т.е. я знаю на уровне идеи как это написать, аналогичное уже было написано и использовалось при поиске магических квадратов, осталось сесть и написать всё, включая самое главное — правильную инициализацию процесса перебора. Но тут работы навалилось и свободного времени нет ...
VALНикак у меня не дойдут руки детально проанализировать собранную статистику о пользе подстановки в модуль квадратов простых. Уже неделю лежит. Потому выложу как есть, лишь с небольшими комментариями.
Исследовалось на простом модельном паттерне без оптимизирующих проверок на делимость на малые простые — всё ради более частого выполнения условий делимости и псевдопростоты, для набора статистики. Паттерн следующий:
\\ n+0 n+1 n+2 n+3 n+4 n+5 n+6 n+7 n+8 n+9 n+10 n+11 n+12 n+13 n+14
\\%32: %25 %26 %27 %28 %29 %30 %31 %0 %1 %2 %3 %4 %5 %6 %7
\\Без подстановки 2645:
? v=[ 1, 722, 1, 1, 1, 1, 1, 32, 1, 1, 1, 1, 1, 98, 1 ]; pp=Mod(25,64); for(i=1,#v, pp=chinese(pp,Mod(-i+1,v[i]))); print(pp);
Mod(188441, 1132096)
\\С подстановкой 2645:
? v=[ 1, 722, 1, 1, 2645, 1, 1, 32, 1, 1, 1, 1, 1, 98, 1 ]; pp=Mod(25,64); for(i=1,#v, pp=chinese(pp,Mod(-i+1,v[i]))); print(pp);
Mod(2807786521, 2994393920)
В остальном программа не отличалась (специально сделал похожей на Вашу):
Код:
{n0=0; n1=0; n2=0; n3=0; n4=0; n5=0; mm=pp.mod/722; st=(ceil(1e40/pp.mod)*pp.mod+lift(pp)+1)/722;
for(i=0,10^9-1,
p=st+i*mm; n0++;
if(!ispseudoprime(p), next);
n=722*p-1; n1++;
if(ispseudoprime((n+7)/32) && ispseudoprime((n+13)/98),
n2++; if((n+4)%2645==0, n3++; if(ispseudoprime((n+4)/2645), n4++)); if(numdiv(n+4)==12, n5++); DispIf(n);
);
);
print("Num=",n0,", prime19=",n1,", test=",n2,", div=",n3,", prime=",n4,", numdiv=",n5);}
\\Для проверки, без подстановки 2645:
10000000000000000000000000092932350135321: 16, 12, 16, 12, 12,192, 12, 12, 64, 16,128, 12, 32, 12, 48, len=7
10000000000000000000000000357301276013721: 32, 12, 16, 12, 12, 12, 8, 12, 64,128, 12,384, 32, 12,192, len=7
10000000000000000000000000560136707614425: 12, 12, 16, 12, 12,128, 64, 12, 16, 4, 4, 24, 8, 12, 12, len=7
\\Для проверки, с подстановкой 2645:
10000000000000000000000156142307231891481: 8, 12, 32, 12, 48, 12, 32, 12, 8, 32, 12, 48, 4, 12, 12, len=7
10000000000000000000000405361329400792601: 12, 12, 8, 12, 12,384,128, 12, 16,384, 16, 12, 16, 12, 8, len=7
10000000000000000000000616302211592763161: 12, 12, 16,144, 12, 16,128, 12, 4,192, 16, 12, 64, 12, 12, len=7
10000000000000000000000741907170008796761: 12, 12, 32, 12,384, 16,512, 12, 12,128, 32, 96, 16, 12, 12, len=7
10000000000000000000001141901139544651161: 8, 12, 16, 12, 12, 32, 16, 12, 24,256, 12, 12, 16, 12, 96, len=7
10000000000000000000001836845425491398361: 8, 12, 16, 12,192, 64, 32, 12, 12, 32, 12, 12, 32, 12,128, len=7
10000000000000000000002121610475675076761: 16, 12, 8, 12,192, 32, 12, 12, 32,512, 16, 12, 16, 12, 12, len=7
10000000000000000000002245404559396020761: 8, 12, 8, 12, 12, 32,128, 12, 16, 64, 4, 12, 32, 12, 12, len=7
10000000000000000000002387807124469169561: 12, 12, 8, 12, 96, 32, 64, 12, 16,256, 32, 12, 32, 12, 12, len=7
10000000000000000000002664845485497588761: 48, 12, 12, 12,128, 16, 96, 12, 16,128, 16, 12, 32, 12, 12, len=7
Объём перебора составил

разных

в

с наименьшим подходящим

.
Проверялись следующие величины (без подстановки 2645 / с подстановкой 2645):
1. Количество

(т.е. возможных цепочек) на проверку:
1000000000 / 1000000000 (разницы очевидно быть и не должно, оставлено для контроля).
2. Сколько из них оказались простыми (ispseudoprime(p)):
27284151 / 35653087 — разница вызвана разными

и

.
3. Сколько из них проходит тест на простоту после деления на 32 и 98 (и требуют дальнейшей проверки на количество делителей прочих чисел):
29392 / 83768. Все они отправлялись на вычисление делителей всех чисел (выполнялось в DispIf()) для пунктов 6 и далее.
4. Сколько из них оказывается кратными 2645 на месте

:
29 / 83768 (вторая цифра очевидна, оно так по построению).
5. Сколько из них после деления оказались простыми:
3 / 3426.
6. Длины трёх найденных цепочек без подстановок: 4,6,4 — только в одной из трёх ещё какие-то позиции тоже дали ровно 12 делителей.
7. Сколько из цепочек из пункта 3 (т.е. прошедших проверку на прочие числа, но до проверки на 2645) дали ровно 12 делителей на месте

:
490 / 3426 (вторая цифра опять очевидна по построению).
8. Максимальная длина найденных цепочек после прохождения пункта 3:
7 / 7, 3 и 10 штук соответственно (все приведены в листинге программы). Причём пункт 4 прошли лишь 4 цепочки из варианта с подстановками, т.е. в остальных на месте

стоит какое-то другое не кратное 2645 число.
9. Количество найденных цепочек длины 6:
80 / 236.
10. Из-за большой разницы чисел в пункте 3 и соответственно сильно разным временем работы вариантов теста отдельно проверялось влияние служебных операций на время работы, на сокращённом переборе в

разных

с удалённой строкой кода правее n2++ время счёта составило:
36.2с / 45.5с. Влиянием инкремента счётчиков пренебрёг. Практически всю разницу можно списать на разное количество простых в диапазонах в пункте 2.
Предварительные выводы.
Из пункта 3 следует что на каждые миллиард цепочек лишь от 30 до 85 тысяч требуют дополнительной проверки на количество делителей прочих чисел, в зависимости выполнялась или нет соответственно подстановка квадратов малых простых в паттерн с увеличением модуля. Именно этот результат в общем и интересовал.
Из него же следует что любая дополнительная проверка займёт в общем времени работы долю

или менее 0.01%. Даже если она будет в
сто раз дольше первых проверок, всё равно общее замедление составит лишь 1%, что считаю явно несущественным. Т.е. добавление проверок на не подставленные квадраты простых в первом варианте на общем времени работы сказываться практически не должно.
Из разницы для первого варианта цифр в пунктах 5 и 6 видно что в 487 цепочках из 490 на месте

стоит другая
допустимая комбинация простых, не 2645q. Ограничение перебора лишь кратными 2645 приводит к сокращению находимых цепочек на два порядка. Вероятно примерно аналогичные цифры будут и для других подставляемых чисел. Но важность этого вывода
весьма спорна, ведь пункты 8 и 9 показывают что после подстановки количество кандидатов выросло втрое.
В итоге ситуация двойственная: с одной стороны без подстановки найдено на два порядка больше разных кандидатов в каждом конкретном месте паттерна, с другой стороны на всех 15-ти местах кандидатов втрое меньше. Плюс подстановка приводит к росту чисел и замедлению работы PARI. Что полезнее реально я не понимаю. На первый взгляд очевидных
кардинальных преимуществ нет ни у одной из сторон.
Ну и никаких отличий в

не обнаружено.

Возможно из-за слишком простого метода проверки и маленького объёма перебора.

 .
.  не сравнимо с 17 по модулю 37
не сравнимо с 17 по модулю 37 ,
,  и
и  ). И мне понадобился гораздо меньший шаг, чем
). И мне понадобился гораздо меньший шаг, чем  . Впрочем, для подробных объяснений время ещё не пришло.
. Впрочем, для подробных объяснений время ещё не пришло. (или
(или  как у
как у  в час). Замечательно что при этом величина самих чисел вообще не важна, все операции кроме начальной настройки производятся в поле (кольце?) модулей. Т.е. я знаю на уровне идеи как это написать, аналогичное уже было написано и использовалось при поиске магических квадратов, осталось сесть и написать всё, включая самое главное — правильную инициализацию процесса перебора. Но тут работы навалилось и свободного времени нет ...
в час). Замечательно что при этом величина самих чисел вообще не важна, все операции кроме начальной настройки производятся в поле (кольце?) модулей. Т.е. я знаю на уровне идеи как это написать, аналогичное уже было написано и использовалось при поиске магических квадратов, осталось сесть и написать всё, включая самое главное — правильную инициализацию процесса перебора. Но тут работы навалилось и свободного времени нет ... разных
разных  с наименьшим подходящим
с наименьшим подходящим  .
. и
и  .
. :
:  разных
разных  или менее 0.01%. Даже если она будет в
или менее 0.01%. Даже если она будет в  не обнаружено.
не обнаружено.  .
.  , а не
, а не  , но это работает.
, но это работает. (а не
(а не  ) чисел по
) чисел по  делителей. Первое число —
делителей. Первое число —  .
. огромных простых. А что мы про них знаем?
огромных простых. А что мы про них знаем? из них точно дают произведения:
из них точно дают произведения:  ,
,  ,
,  ,
,  ,
,  . Например, про самое большое,
. Например, про самое большое,  известно, что три последних десятичных цифры не выходят за пределы этого набора:
известно, что три последних десятичных цифры не выходят за пределы этого набора:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. , а не
, а не  . То есть всё-таки ставить 7-ку на 4-е либо 12-е место. Ибо подходящих простых в этом случае пока находится в
. То есть всё-таки ставить 7-ку на 4-е либо 12-е место. Ибо подходящих простых в этом случае пока находится в  раза больше. Опять-таки, подробнее пока не буду.
раза больше. Опять-таки, подробнее пока не буду. .
. ,
,  , ...,
, ...,  .
. -ка должна стоять. Но только с 5-й попытки все простые попадают на свои места.
-ка должна стоять. Но только с 5-й попытки все простые попадают на свои места. -к. И только их. Вот это и есть 4-кратное превосходство такой расстановки.
-к. И только их. Вот это и есть 4-кратное превосходство такой расстановки. ) пока не берусь, но надежды радужные.
) пока не берусь, но надежды радужные. ) сильно быстрее
) сильно быстрее  вместо
вместо  , но тут объяснение может быть проще (хотя и предыдущее про
, но тут объяснение может быть проще (хотя и предыдущее про  тоже подходит): надо чтобы при делении на
тоже подходит): надо чтобы при делении на  получалось нечётное число ибо чётными простые быть не могут (а
получалось нечётное число ибо чётными простые быть не могут (а  уже задействована).
уже задействована). , где
, где  .
. : из
: из  последовательных индексов
последовательных индексов  ,
,  ).
). ) и сделать распараллеливание на все доступные ядра (или явно указанное количество) и можно выкладывать.
) и сделать распараллеливание на все доступные ядра (или явно указанное количество) и можно выкладывать. (сделать до
(сделать до  тоже не слишком сложно). Ни
тоже не слишком сложно). Ни  .
. в
в  и нашла лишь три десятки (10 чисел из 15 имеют ровно 12 делителей), более короткие не считаю.
и нашла лишь три десятки (10 чисел из 15 имеют ровно 12 делителей), более короткие не считаю. встречаются в 8 раз реже, чем для
встречаются в 8 раз реже, чем для 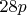 . И я уже стал подозревать, что имеется принцип наименьших множителей и надо распространить его и на другие числа.
. И я уже стал подозревать, что имеется принцип наименьших множителей и надо распространить его и на другие числа. соответственно. Здесь
соответственно. Здесь  — 4 пары различных простых. Вроде бы выбрал самые маленькие множители. Но в законности такого расположения немного сомневаюсь.
— 4 пары различных простых. Вроде бы выбрал самые маленькие множители. Но в законности такого расположения немного сомневаюсь.