Вероятность чётного суммарного счёта в матче

[melnikoff]

Школьная задачка:
По результатам многолетних наблюдений известно, что средний суммарный счёт (общее число забитых мячей) в матчах между командами "Физик" и "Лирик" равно 2.
На сколько вероятность того, что следующий матч между этими командами окончится с чётным суммарным счётом больше вероятности того, что суммарный счёт будет нечётным?

Попытка:
Такое ощущение, что условия неполные, так как
$2 = \frac{2+2}{2} = \frac{1 + 3}{2}$.
Если же под "По результатам многолетних наблюдений" подразумевается, что распределение матчей по суммарному счёту является унимодальным, то всё равное не очень понятно как решать.

[lel0lel]

А точно ли задача школьная? Так-то распределение Пуассона нужно применять.

[mihaild]

Откуда следует, что число забитых мячей распределено по Пуассону? (или какому-то еще распределению конкретного вида)
ИМХО действительно условия неполны.

[lel0lel]

Ниоткуда, более того, Пуассона быть не может, как и любого другого распределения с неограниченным числом успехов. Но решать то как-то надо, тем более параметр задан единственный, а потому Пуассон и вероятность считаем с точностью до сотых.

[mihaild]

(Оффтоп)

lel0lel в сообщении #1548339 писал(а):

Но решать то как-то надо

Сомневаюсь.

lel0lel в сообщении #1548339 писал(а):

а потому Пуассон

А почему не дельта? Решать проще будет.

lel0lel в сообщении #1548339 писал(а):

и вероятность считаем с точностью до сотых

Почему это? Если уж предположить Пуассона, то можно и точно посчитать.

[lel0lel]

mihaild в сообщении #1548340 писал(а):

А почему не дельта? Решать проще будет.

Нереалистично.

mihaild в сообщении #1548340 писал(а):

Почему это? Если уж предположить Пуассона, то можно и точно посчитать.

Можно ради математического любопытства. А так, я не помню, чтобы были матчи с числом голов больше сотни.

Вот представьте Вы работаете аналитиком некой букмекерской конторы, и приносят такую задачу с неполными данными (другой статистики нет), просят дать какие-нибудь оценки. Зарплату платят хорошую. Какое бы распределение выбрали?

[Евгений Машеров]

Условие сильно неполное. Скажем, не указано, что силы команд равны. А ведь можно рассмотреть вариант, когда одна команда всегда всухую проигрывает, а забивает лишь вторая. Но и в этом случае вторая может всегда забивать 2 года, а может поровну 1 и 3. Соответственно вероятность чётного в следующем матче может быть 100%, а может быть 0%.
Впрочем, можно и при равной силе рассмотреть, когда команда-неудачник выбирается с вероятностью 0.5, а победитель забивает то ли 2 гола, то ли то 1, а то 3.
Можно дополнить, сказав, что событие "забили гол команде Х" случайное, с равными вероятностями для обеих команд. Но это условие надо явно оговаривать.

[melnikoff]

Задача с сайта Вероятность в школе (вторая сверху).

[mihaild]

lel0lel в сообщении #1548341 писал(а):

Нереалистично

Сойдет. Играем до двух очков.

(Оффтоп)

lel0lel в сообщении #1548341 писал(а):

Вот представьте Вы работаете аналитиком некой букмекерской конторы, и приносят такую задачу с неполными данными (другой статистики нет), просят дать какие-нибудь оценки. Зарплату платят хорошую. Какое бы распределение выбрали?

Если я работаю аналитиком, а статистики нет, то я выберу распределение в другую букмекерскую контору, эта всё равно скоро разорится.

[waxtep]

melnikoff в сообщении #1548333 писал(а):

средний суммарный счёт (общее число забитых мячей)

Это видимо значит не то, что в среднем Ф забивает на два мяча больше, чем Л, а что популярны исходы 2:0, 1:1 и 0:2

-- 09.02.2022, 00:47 --

Хотя все равно не помогает

[Александрович]

melnikoff в сообщении #1548333 писал(а):

По результатам многолетних наблюдений известно, что средний суммарный счёт (общее число забитых мячей) в матчах между командами "Физик" и "Лирик" равно 2.
На сколько вероятность того, что следующий матч между этими командами окончится с чётным суммарным счётом больше вероятности того, что суммарный счёт будет нечётным?

Если принять что исходы по суммарному счёту равновероятны, то на 0,2.

[melnikoff]

Александрович в сообщении #1548354 писал(а):

Если принять что исходы по суммарному счёту равновероятны, то на 0,2.

А правильный ответ (или "правильный") 0,0183.

[Александрович]

melnikoff в сообщении #1548376 писал(а):

А правильный ответ (или "правильный") 0,0183.

Такой ответ получается, если принять что исходы по суммарному счёту распределены по закону Пуассона.

[Евгений Машеров]

Александрович в сообщении #1548354 писал(а):

Если принять что исходы по суммарному счёту равновероятны, то на 0,2.

"Исходы по суммарному счёту" не могут быть равновероятны. Поскольку без дополнительных ограничений указать верхнюю границу числа забитых мячей мы не можем, и получаем несобственное распределение. Можно ввести ограничение, состоящее в том, что игра ведётся до N забитых голов, но оно не соответствует правилам футбола и, во всяком случае, делает ответ зависимым от неуказанного N.
Привлекая "внематематические соображения", видим, что задача (я по ссылке самой задачи не увидел) с сайта МЦНМО, который "не только школьный", но если школьный, то для кружковой работы или самостоятельной подготовки. То есть привлечение сведений, заведомо не входящих в школьную программу, возможно. В частности, могут рассказать о распределении Пуассона ("законе малых чисел" по Борткевичу), обосновывая тем, что в ходе игры возникают ситуации владения мячом, завершающиеся голом с вероятностью $p\ll 1$. Тогда получаем число голов, забитых каждой командой, распределённое по Пуассону , и суммарное тоже по Пуассону. 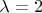Для суммарного $\lambda=2$ по свойству матожидания пуассоновского распределения и дальше тупо считать. Судя по совпадению ответа - рассуждали именно так.

[lel0lel]

Всё-таки Пуассон) обычно такие задачи включают в учебник сразу после пройденного материала, поэтому какое распределение выбирать понятно.