Здравствуйте, читаю учебник по функциональному анализу и не могу понять, как я умудрился доказать ложное утверждение. Где-то должна быть ошибка в рассуждениях, вероятно, при переходе от образа к прообразу и наоборот, но я всё равно не очень понимаю в чём проблема.
Утверждение:

Доказательство:
Пусть

, и

, тогда,

, то есть

и
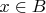
. Тогда,

и

, то есть

.
С другой стороны, если

, то

и

, то есть

и
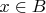
. Тогда,

, то есть

.
Заранее благодарю за ответ!