Тогда
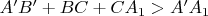
.
Why is this inequality correct? Are you use some inequalities between the triangle sides?
I think from what was written by
TOTAL I finally understand a solution. (I've seen 3 ideas to solve the problem.)
What is on the picture is surrounding surface after cut on one of the edges OA, OB, OC and put on a plane. The condition
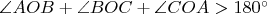
is used when the surface is unfolded on the plane to say
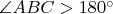
.
"Красное
больше сине-желтого
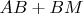
" the reasoning can be multiple (3) times applying an inequality between the triangle's sides.
* 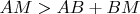
"Синее - два края разрезанного ребра." - because we are cutting on an edge and unfolding - on the picture
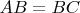
.
"Желто-красное
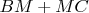
больше синего
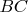
." - because of the triangle
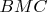
and many (2) times applying the triangle inequality for the red segments we have
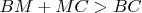
. (The sum of two sides in a triangle is always greater than the third side).
** 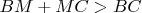
"Складывая, получаем, что синее короче красного" - Summing
* and
** we have:
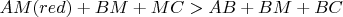
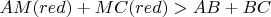
triangle's perimeter
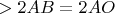
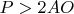
The desired result.
Looks like it is one of the most obvious not obvious problems.