Мы же здесь полагаем, что
1) оптимальная стратегия есть,
2) оба игрока ее придерживаются,
3) оба осведомлены о п. 2?
Игрок бросает кости, и по результатам броска двигает фишку, с вероятностью

на одну лунку, с

- на две лунки вперед. А с вероятностью

- выбирает лунку из этих двух. Оптимальная стратегия означает, что он выбирает так, чтобы его соперник, начинающий с новой лунки, имел более низкие шансы на победу, чем в альтернативном случае.
В случае (а) замечаем:
Если перед ходом игрока фишка находится в лунке 12, то он сразу проиграл,

Если - в лунке 11, то он с вероятностью

получает перебор, в противном случае либо автоматически попадает в целевую лунку, либо выбирает ее из двух (дилемма простая: перебор или победа, и решается очевидным образом). Таким образом,

.
Пусть фишка в лунке

. Тогда (повторюсь, на этот раз с числами) с вероятностью

фишка немедленно попадет в клетку

, где вероятность
его поражения равна

, с той же вероятностью в клетку

, вероятность поражения

. А в прочих случаях (вероятность

) он выбирает. Здесь вероятность поражения равна

.
Таким образом, рекуррентная формула для вероятности победы при начале в лунке

выглядит так:

(если круг состоит не из 12, а из много большего количества лунок, то на достаточно большом расстоянии до финиша вероятности ожидаемо осциллируют около

)
Используя вычисленные ранее значения

, получим, что

.
В случае (б) есть небольшое изменение: при "проскоке" фишка оказывается в лунке 1, с которой начинает соперник, то есть вероятность победы - это вероятность поражения соперника, в итоге

. Но исходно

нам неизвестна (хотя уже можно предполагать, что близка к

), и получается система из 11 уравнений с 11 неизвестными. Была бы она линейной, было бы здорово. Но модуль (или
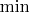
) портят всю малину. Здесь понадобится либо догадка о соотношении вероятностей для соседних лунок, по критерию "больше-меньше", либо итеративные вычисления

. Второе проще, если решать численно, и получается

.



