Здравствуйте.
Не получается получить формулу Гаусса как это делается в книге "Позняк, Шикин, Дифференциальная геометрия: первое знакомство". Рассматриваем разложение

Далее имеем

Уравнение

должно дать теорему Гаусса

Здесь

. Я выражал

через коэффициенты первой квадратичной формы

, их первые и вторые производные, а также через коэффициенты второй квадратичной формы

, но уравнение

к вышеприведённой теореме Гаусса не привело. Чтобы не расписывать всё полностью, посмотрим, какие выражения, содержащие только коэффициенты первой квадратичной формы и их производные получаются при коэффициенте

. Поскольку символы Кристоффеля устроены как

умноженное на сумму произведений коэффициента первой квадратичной формы на первую производную от коэффициента первой квадратичной формы, то достаточно рассмотреть только первые два слагаемые в

, имеем

Тогда выражение

, содержащее

у меня получается такое

А в теореме Гаусса выражение, содержащее

получается таким

То есть, вторая скобка в выражении
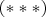
получается лишней.
Выражения

и

, я проверял, у меня получились такие же. Также я посмотрел книгу "Погорелов. Дифференциальная геометрия", там теорема Гаусса записывается так же само.