Имеем последовательность

где

это
A014081, а

это
A053645. После небольшой инспекции отмечаем следующее:
Чтобы достаточно просто получить подпоследовательность позиций членов со значением

, начните с наименьшего

, такого

, а затем используйте правило, такое же, как и для
A003714: если

находится в последовательности, то в ней также есть как

, так и

. Гипотеза: подпоследовательность совпадает с последовательностью только в том случае, если
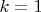
или

где

- простое число (в остальных случаях требуются дополнительные значения, например при

это

где

).
Можно ли это как-нибудь доказать (или опровергнуть контрпримером)?
Иначе контрпример можно сформулировать так: два значения

, такие, что

для некоторого простого

.



