Решал тут следующий пример. Да не только он, но во многих у меня есть следующий вопрос.

найти Изображение, пользуясь преобразованием Лапласа.

Неопределенный интеграл
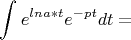

Далее дело техники о пределах, но вот тут то и вопрос. Как предел считать, зная что

любое комплексное выражение, лежащее в полуплоскости

где

показатель роста,
а значение

может быть любое. Т.е. я нахожусь в неопределенности, что делать с

и

. Помогите сдвинуться с данной мертвой точки, что делать нужно далее, как учитывать

и

в пределе.
Предел волнует на бесконечности