Здравствуйте, форумчане. Столкнулся с задачей по гидродинамике. Необходимо определить распределение скоростей и давлений в несжимаемой, идеальной жидкости, которая подается в сужающийся усеченный конус, при этом жидкость предварительно закручена, и до входа в конус имеет постоянную угловую скорость. В процессе прохождения по конусу жидкость не только увеличивает скорость поступательного движения, но и вращательного (по закону сохранения момента импульса)
Для решения поставленной задачи решил исходить из уравнений Эйлера для жидкости:



Каждому элементарному объему жидкости соответствуют определенные значения

в декартовой системе координат, и

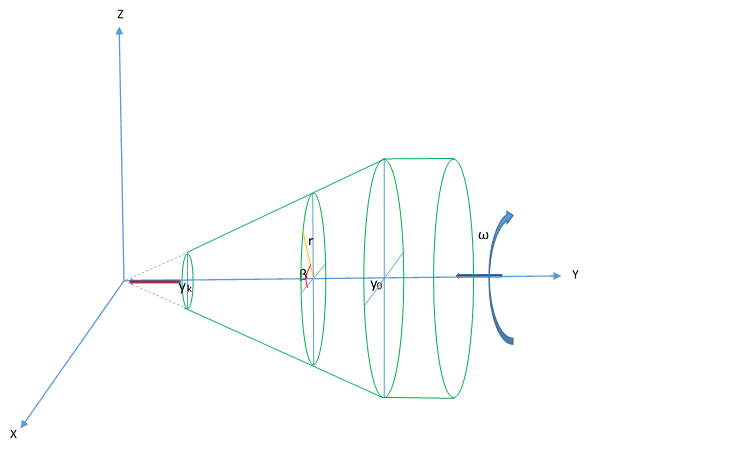
в новой (не знаю, как правильно ее назвать (конической(?)) системе координат. Из рисунка можно видеть:

. Тогда:



Где

Находим частные производные компонент скоростей по координатам, как функции

:




Тогда

Аналогично:



Используя первое из уравнений Эйлера (1), с учетом (2-5) найдем проекции ускорений на ось

. Для угла

:

Это ускорение обусловлено центростремительной силой, которая в силу симметрии не зависит от угла

. Поэтому можно записать:

Для угла

:

Очевидно, что это ускорение равно нулю (т.к. давление для постоянного

и

с изменением угла

не меняется). Поэтому

Далее,

После подстановки соответствующих производных во второе уравнение Эйлера (1) упрощений и сокращений, получаем:

Принимая, что давление является непрерывной функцией от

и

, и существуют его частные производные до второго порядка справедливо соотношение:

Тогда дифференцируя левую часть выражения (6) по

, а левую часть (8) по

, и приравнивая получаем:


Уже есть два дифференциальных уравнения и три неизвестных функции, подлежащие определению:

Есть еще одно условие описываемое уравнением:

, которое после соответствующих подстановок для нашего случая приобретает вид:

От смешанных производных в уравнении (9) можно избавиться, используя уравнение (10). Возникают следующие вопросы: 1) Хватает ли уравнений 7), 9) и 10) для определения искомых функций, при надлежащем выборе граничных условий; 2) Как выбрать дополнительные граничные условия, кроме этих:

; 3) Можно ли решить эту систему уравнений средствами маткад 15, если нет, то что можно применить?