Не могу никак объяснить который раз. Тот простой палиндром, который Вы найдёте придется проверять из каких чисел он состоит. Если он никак не состоит из простых близнецов, то он, хоть и простой палиндром, но ничем не помогает в нашей задаче. Далее ищете следующий, следующий, ... проверяете, проверяете, ... пока не найдёте тот простой палиндром, который будет состоять из простых близнецов.
Хм. У меня всё время было впечатление, что Вы ищете любые простые палиндромы, и Вы почему-то убеждены, что их проще получать, используя пары простых близнецов. И, похоже,
Dmitriy40 пребывал в том же заблуждении.
вычислить простой 35-значный палиндром, составленный из простых близнецов, перебрав

комбинаций вставок

попыток на один
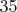
-значный палиндром? Что-то многовато. Плотность простых чисел в районе

равна примерно

. Учитывая, что заранее отброшены все числа, кратные

или

, плотность простых среди оставшихся нужно умножить на

, и получится

. Плотность простых среди палиндромов, начинающихся (и оканчивающихся) на цифры

, должна быть примерно такой же, поэтому на один простой палиндром должно тратиться в среднем примерно

попытки. Эта оценка должна быть немного завышенной, так как относится к верхней границе множества
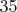
-значных чисел.
Я проделал численный эксперимент, вычислив

случайных простых
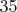
-значных простых палиндромов. Процессор двухъядерный, тактовая частота

GHz, используется система компьютерной математики Wolfram Mathematica 11.3.
Палиндромы генерируются командами
![$\mathrm{Lst = Append[RandomChoice[Range[0, 9], 17], RandomChoice[\{1,3,7,9\}]];}$ $\mathrm{Lst = Append[RandomChoice[Range[0, 9], 17], RandomChoice[\{1,3,7,9\}]];}$](https://dxdy-01.korotkov.co.uk/f/4/1/9/4192219ffeee8dc1e00c7e1bf9bbe2ec82.png)
![$\mathrm{Lst = Join[Reverse[Delete[Lst, 1]], Lst];}$ $\mathrm{Lst = Join[Reverse[Delete[Lst, 1]], Lst];}$](https://dxdy-04.korotkov.co.uk/f/b/d/c/bdc4f13ca86b6a5fe06d2adc98ac203b82.png)
![$\mathrm{p = FromDigits[Lst];}$ $\mathrm{p = FromDigits[Lst];}$](https://dxdy-03.korotkov.co.uk/f/e/9/6/e96da9c68a952759256d97c9b2f1375482.png)
Далее построенный палиндром проверяется на простоту, подсчитывается количество сгенерированных палиндромов и количество простых среди них.
В итоге для получения

простых потребовалось проверить

палиндромов, то есть, в среднем

проверок на один простой палиндром.
Затраты времени составили

секунды.
Последний найденный простой палиндром равен

.