Никак не пойму почему поле внутри конденсатора конечных размеров считатся однородным, а вне пластин конденсатора оно нулевое.
Берем например заряженную пластину радиуса R . Напряженность электрического поля Е по оси z перпендикулярной центру :
![$E=\frac{\sigma}{2\varepsilon_0}\left[1-\frac{z}{\sqrt{z^2-R^2}}\right]$ $E=\frac{\sigma}{2\varepsilon_0}\left[1-\frac{z}{\sqrt{z^2-R^2}}\right]$](https://dxdy-04.korotkov.co.uk/f/3/4/1/3414ab85c23f7cae49caa5ca8a22365382.png)
Если мы возьмем 2 пластины и поставим их соосно на расстоянии d друг от друга, то напряженность в каждой точке вне пластин это будет сумма напряженностей от каждой пластины.
Так как заряды на пластинах равные и разного знака то получаем (для точек на оси перпендикулярной пластинам)
![$E=\frac{\sigma}{2\varepsilon_0}\left[1-\frac{z}{\sqrt{z^2-R^2}}\right] - \frac{\sigma}{2\varepsilon_0}\left[1-\frac{z-d}{\sqrt{(z-d)^2-R^2}}\right] $ $E=\frac{\sigma}{2\varepsilon_0}\left[1-\frac{z}{\sqrt{z^2-R^2}}\right] - \frac{\sigma}{2\varepsilon_0}\left[1-\frac{z-d}{\sqrt{(z-d)^2-R^2}}\right] $](https://dxdy-03.korotkov.co.uk/f/2/d/8/2d850d5cc8cb7fadc1b45074bc40080a82.png)
Вот хочу нарисовать график этой функции (убираем лишние константы и раскрываем скобки):

По идее он же должен внутри пластин от z=0 до z=d быть примерно постоянным, а вне плластин быстро падать в 0.
Возьмем d=1 и R=100 (d<<R)
и нарисуем график то получим что поле >0 далеко за пластинами да и вообще оно сильно ослаблено даже между пластинами:
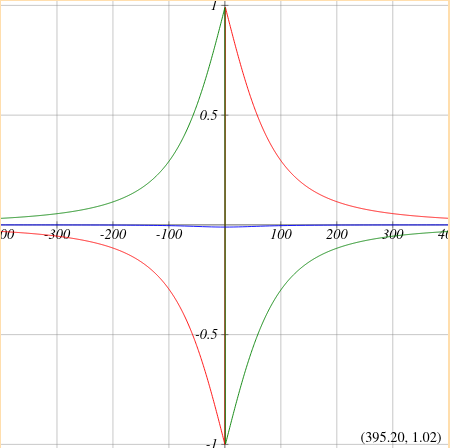
где у меня ошибка?
график рисую тут
http://www1.chapman.edu/~jipsen/svg/asciisvgeditor.htmlКод:
setBorder(0)
s=400
ss=1.02
initPicture(-s,s,-ss,ss)
axes(100, 0.5, "labels",100,0.5)
r=100
d=1
stroke = "red"
plot("(abs(x)/(x+0.000000001))(1-(abs(x)/sqrt((x)^2+r*r)))",0-s,s,1000)
stroke = "green"
plot("(-abs(x)/(x+0.000000001))(1-(abs(x-d)/sqrt((x-d)^2+r*r)))",0-s,s,1000)
stroke = "blue"
plot("\
(abs(x)/(x+0.000000001))(1-(abs(x)/sqrt((x)^2+r*r)))\
+\
(-abs(x)/(x+0.000000001))(1-(abs(x-d)/sqrt((x-d)^2+r*r)))\
",0-s,s,100)
тут (x+0.000000001) чтобы не было деления на ноль и график выглядел чище
abs(x)/(x+0.000000001) - направление поля справа и слева от пластины в разные стороны