Правильно ли я понимаю, что

тут будет

, при этом это и будет нашим сцепленным током?
Нет. Вам нужно делать, как Вы начали делать в первом пункте, только интегрировать не до

, а до какого-то радиуса (вообще говоря, который меньше

), его удобно обозначить буквой

. А так как предел интегрирования и переменную интегрирования обозначать одной буквой не кошерно, то лучше записать так:

Ну и далее всё пересчитать (ответ будет другим).
-- 05.06.2021, 17:29 --где у меня предел, интеграл ещё не взят,
Если у Вас ещё интеграл не взят, то числитель должен быть в степени
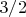
, а не под квадратным корнем (степень

). Тогда и размерность сойдется.
-- 05.06.2021, 17:32 --В первой задаче разве есть разница, течёт ток равномерно или изменяется в разных координатах проводника?
При ответе на вопрос задачи (а там спрашивают про энергию поля в толще проводника) - есть разница и большая.
Пусть весь ток течёт в бесконечно тонком цилиндре по оси проводника. Тогда энергия поля будет бесконечно большой.